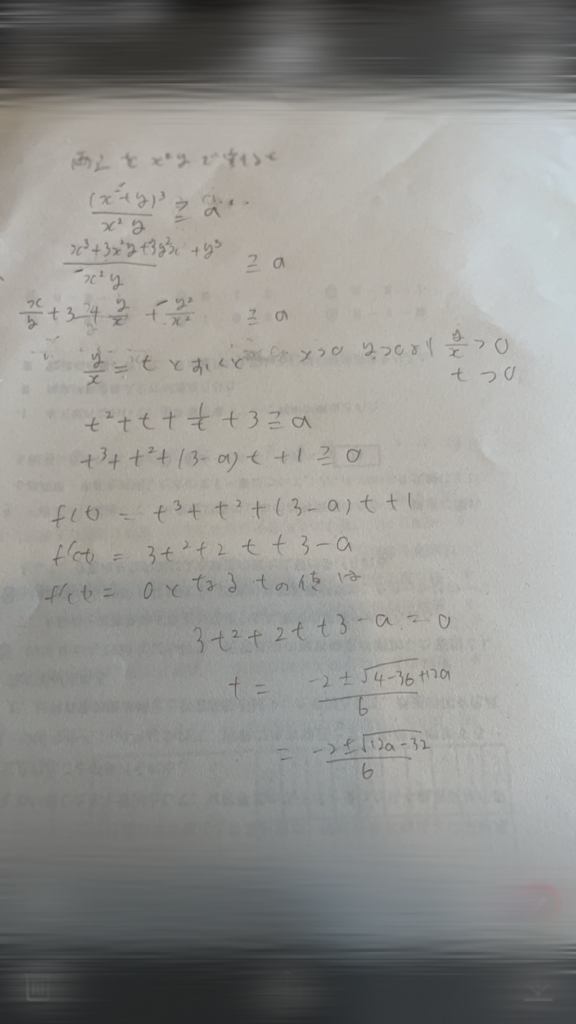今日は・・・特にトップ高の先生たちにとても喜んでいただける”ネタ”です。

 

『次数を下げる』

『対称性・周期性に着目する』

『ゴールからスタートをたどる』

のように・・・・

数学の世界には【どんな問題にも通じる10のアプローチ】が存在します。

これは・・・あくまでも“作問者側”の発想です。

つまり、作問者(大学のそれなりの役職の付いた教授、つまり理学博士)が入試問題を作問するときの

テーマ(主題)をどこに置くか? ということです。

 

東大、京大のような難問に向き合う時などは、その威力は計り知れないものがあります!!

私は、京大25年分の過去問のほとんどは、この『10のアプローチ』で解きました、とい

うよりこのお陰で解けました。

 

今日はその中の一つ・・・・

 

【変数を減らす!!】

 

について説明させてもらいます。

 

問題はコレ『筑波大の過去問』です!!

京大志望の生徒ですら、このように　”手も足も出ませんでした”

とはいえ・・・“2変数➩1変数”　という発想については大ファインプレーです。

t＞0 の条件の下で、なんでもできるようになったのです!!

2変数➩1変数にできたおかげて・・・・

さらに、こんなこともあんなこともできるようになったのです!!

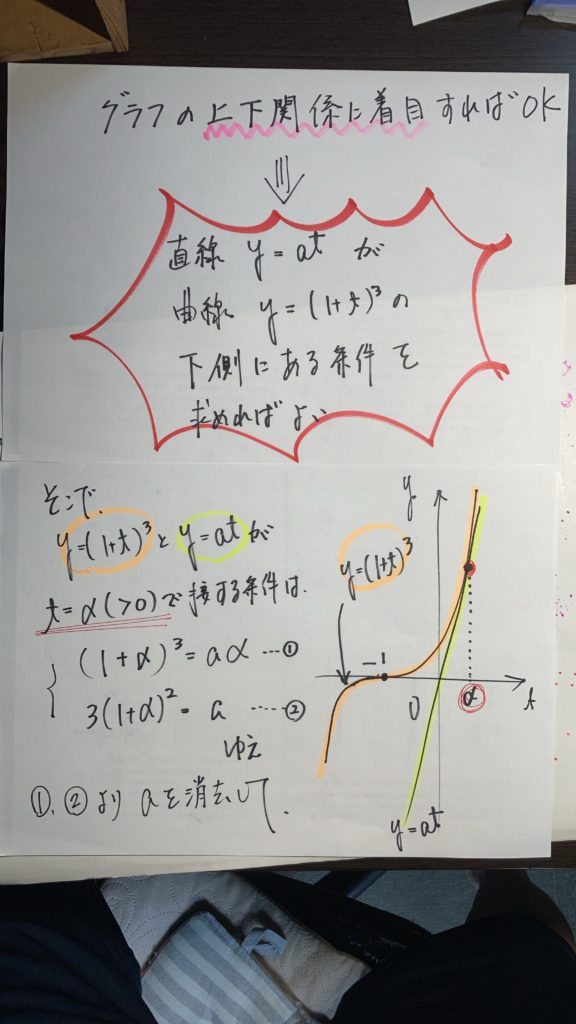
別解を紹介しましょう・・・

 

このタイプの問題・・・・他に2題ご紹介しましょう・・・・

まず・・・下の【2番】

次がコレ・・・微分の応用です。

 

このように見ていくと、

『変数を減らす』というアプローチは、どんな問題にも共通するアプローチの一つであることがお分かりいただけたと思います。

本日、最後まで、読んでいただき、ありがとうございました。