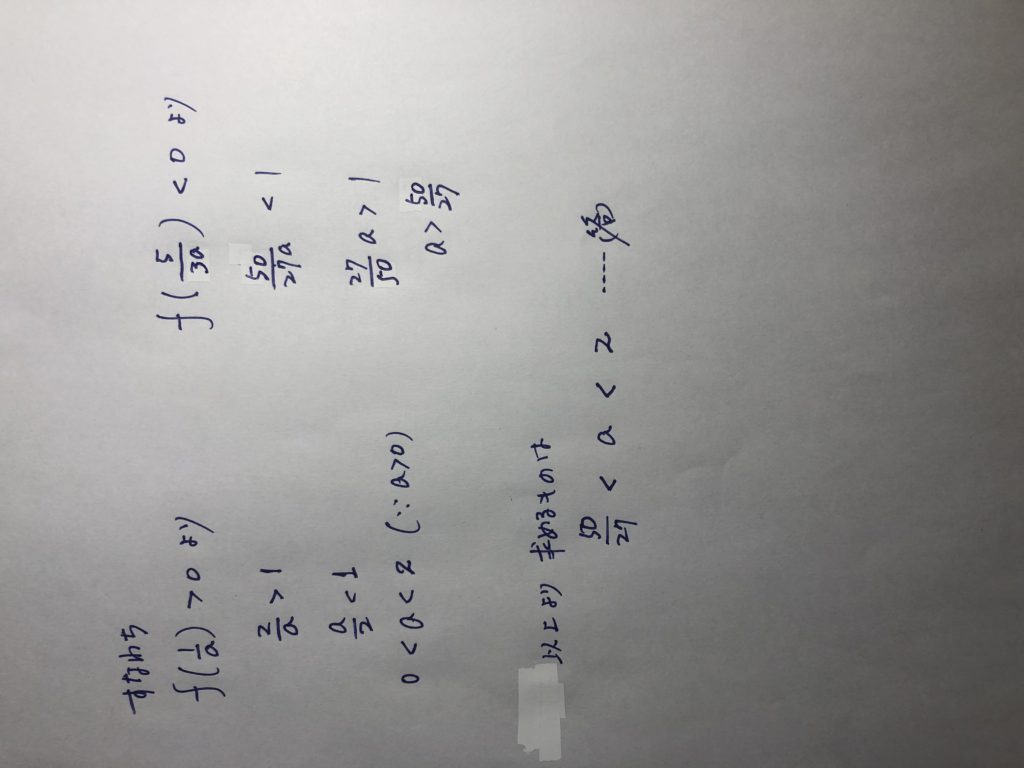さて・・・
やっと、腰をすえて、東大の問題を解く時間を捻出できた・・・
まずは、文系数学から解いてみた。
今年の東大文系数学の中で、一番、とっつきやすく、そして解きやすい一題だったはず。
おそらく、多くの生徒が完答したであろう。
とは言え・・・・・それなりの計算力があっての話だ。
これまでに・・・・
円と放物線の共有点、4個・・・・という問題は、何度か見たが、
円と3次曲線の共有点・・・・・新鮮(?)だった・・・・
北大の文系数学として出題されても、全然違和感のない良問といえる。
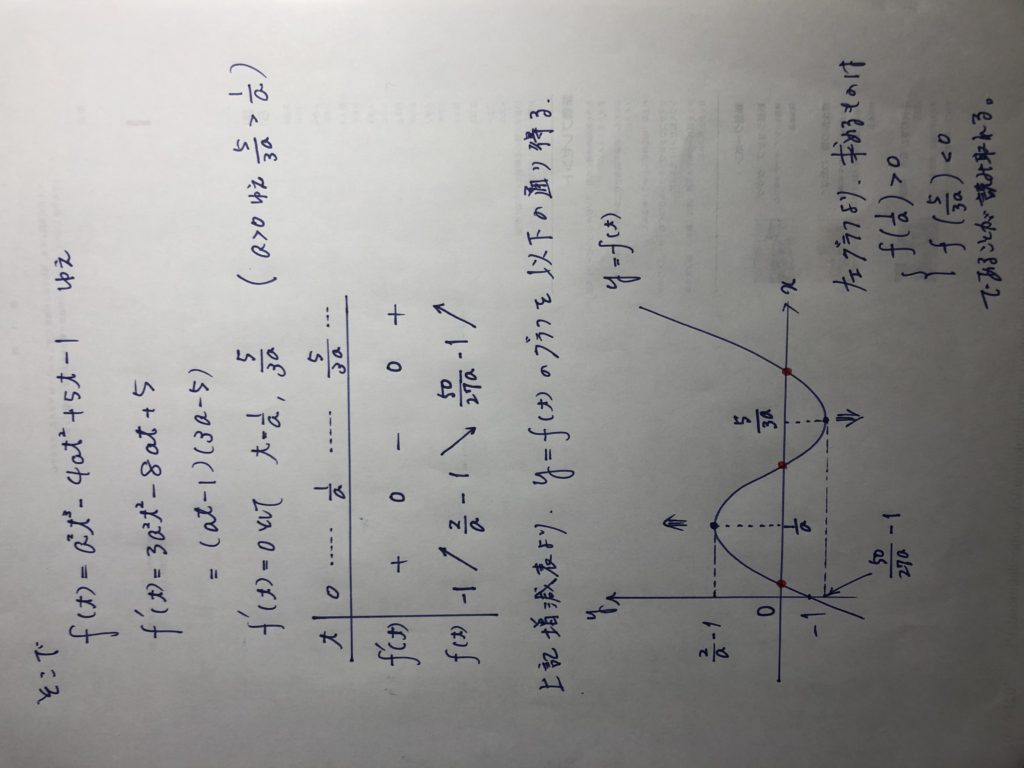
yを消去して得られるχの6次方程式を、tの3次方程式へ書き換え、
t>0 の下で、
実数解3個をもつための条件に帰着させるという王道と言えば王道の問題だ。
◆
◆
◆
今後は、円と3次曲線の融合問題も、ドンドン主流になっていくことだろう。
更には・・・・円と4次曲線で共有点8個・・・・なんてのも登場してくるだろう。
高2生の授業で、とりあげていくことにする!!
日本全国の国立大学の作問担当者は、東大の問題をひとつの模範としている。
本日も、最後まで、読んでいただき、ありがとうございました。