文系、理系問わず、実力養成会の受験生は、
絶対に完璧にマスターしなければならな【必修問題】というものが存在します。
今日は、その一つを紹介させてもらいます。
2014年東大理系、大問1番。
ちまたで、こんなことを聞くときがあります。
“しょせん、東大、京大の問題も、基礎・基本の組み合わせ”
もっともらしく、聞こえますが・・・・間違っています。
“知らないから見えてない”
“見えてる世界でしか、考えれない”
こういうことです。
予備校等で東大クラスを担当する先生たちは、こんなことは、決して言いません。
東大・京大の問題は、
練りに練られ、かつ、じっくりと腰を据えて考えなければ、
手も足も出ません。
ですから、どんな難問にも対応できる”弾力的な応用力”がなければ、
太刀打ちできません。
ちなみに・・・この2014年の東大理系の大問1番、
どこが、基礎・基本の組み合わせなのでしょうか?
私には、よくわかりません・・・・・
今・・・・時代は刻々と変化してます。
20年前、
業界で、あっと驚くような入試問題、
こりゃ・・・・完答は無理!! という入試問題、
こういった入試問題でも、予備校や塾などで【差のつく問題】として
表面的な解答の書き方だけが反復して指導され、
その風潮の中で、かなり勉強に前向きな受験生ですら、
“解法の暗記”に精を出すようになってしまってます。
北大以上の旧帝レベルは、医学部も含め
定型的な解法の暗記は通用しません。
つまり・・・・解法を覚えるのではなく、解法を発見しなければならないのです。
この必修問題は・・・・・
まず・・・・・自ら、座標空間を設定しなければなりません。
問題文を、じっくりと読み、書かれてある事がらを、
座標空間に落とし込み、いかに、解法の糸口を探し出すか?
そこには・・・・それ相応の試行錯誤が必要です。
さらには・・・・空間ベクトルの問題と思いきや、三角関数を経て
フィニッシュは2次方程式の問題に帰着します。
このように・・・本問(東大の問題)は、
単に解くのが難しいという『難問』とは異なり、
苦労のしがいのある良問の極みです。
こういった問題に真正面から向き合うことで、
“どんな難問にも対応できる弾力的な応用力”が培われていきます。
こういった、じっくりと腰を据えて取り組んで欲しい問題を
私は、【必修問題】として受験生へガチで演習させてます。
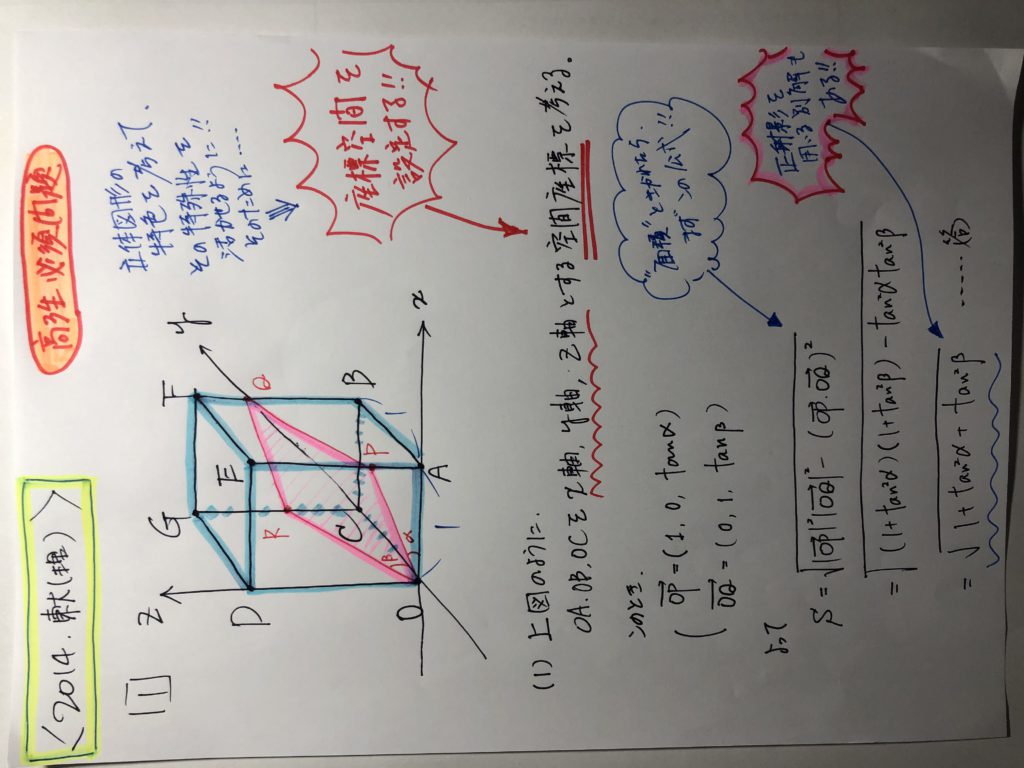
ちなみに・・・本問の解答は次の通りです。
本日も、最後まで、読んでいただき、ありがとうございました。