北嶺中3生より、この問題(数ⅡB)の質問がありました。

このタイプは、もちろん、数ⅡB/4step にも載ってます。

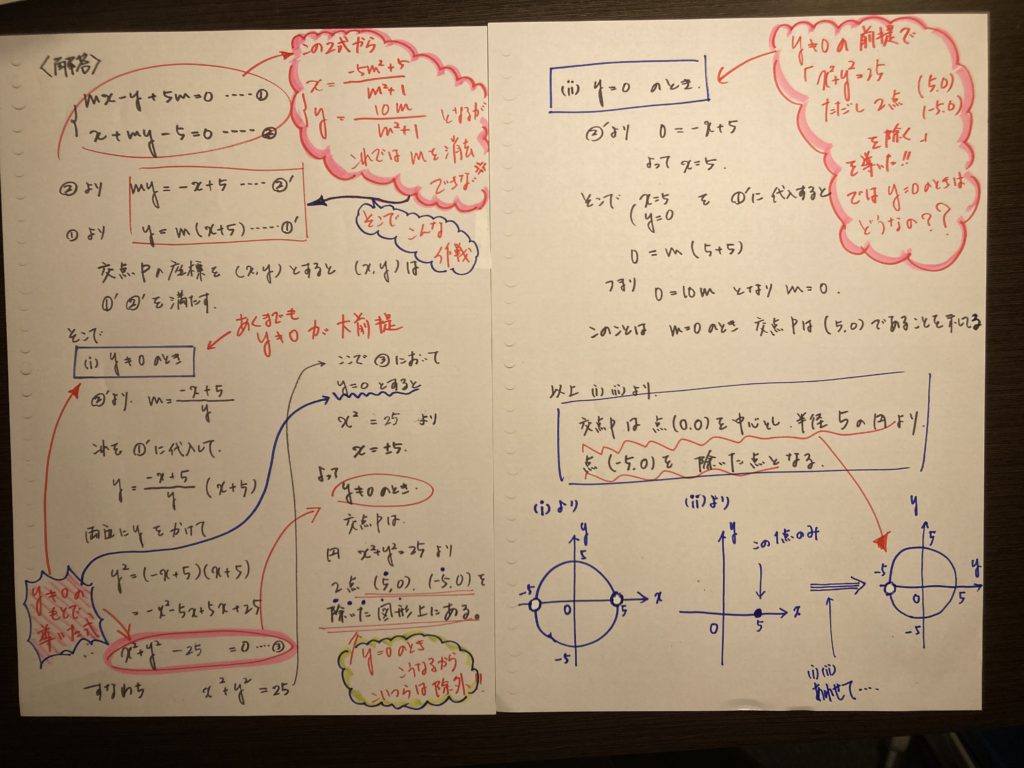
でっ・・・・解答・解説がコレ!!

この他にも　次のような、幾何の知識を用いる初等的な別解もあります!!

論理的にはともかくとして、”運動の直感”により、正しい結論を導くことができます!!

 

生徒からすると・・・・交点　➩　連立方程式の解       という初歩的発想で

χ =

y =

としても・・・・m は消去できない(泣)

 

で・・・・解説に書かれてる方針で行く!!

 

このようなストーリー仕立てなのですが・・・

 

北嶺生が腑に落ちないのは、

『mが消去できない場合はコレで解かざるを得ないのは、わかるけど、

コレって、交点の軌跡を求めるときは”万能”なのか?

それとも・・・”緊急避難的なもの”　なのか?』

 

ここが、”腑に落ちない”　ところです!!

 

 

普段の授業の中で”本質追及”路線で勉強してるので、

北嶺生は、このような視点でこの問題を見てます・・・

 

 

つまり・・・この交点の軌跡は、

交点の存在条件そのもの、

つまり《存在条件が軌跡を軌跡を与える》

 

“存在条件”　の理解が高校数学では、無視・軽視されてるから、

もっと言えば・・・

この種の問題を解くための『述語論理』の運用がなされてない（教科書で触れてない）

ために・・・・・”腑に落ちない”　ということです。

 

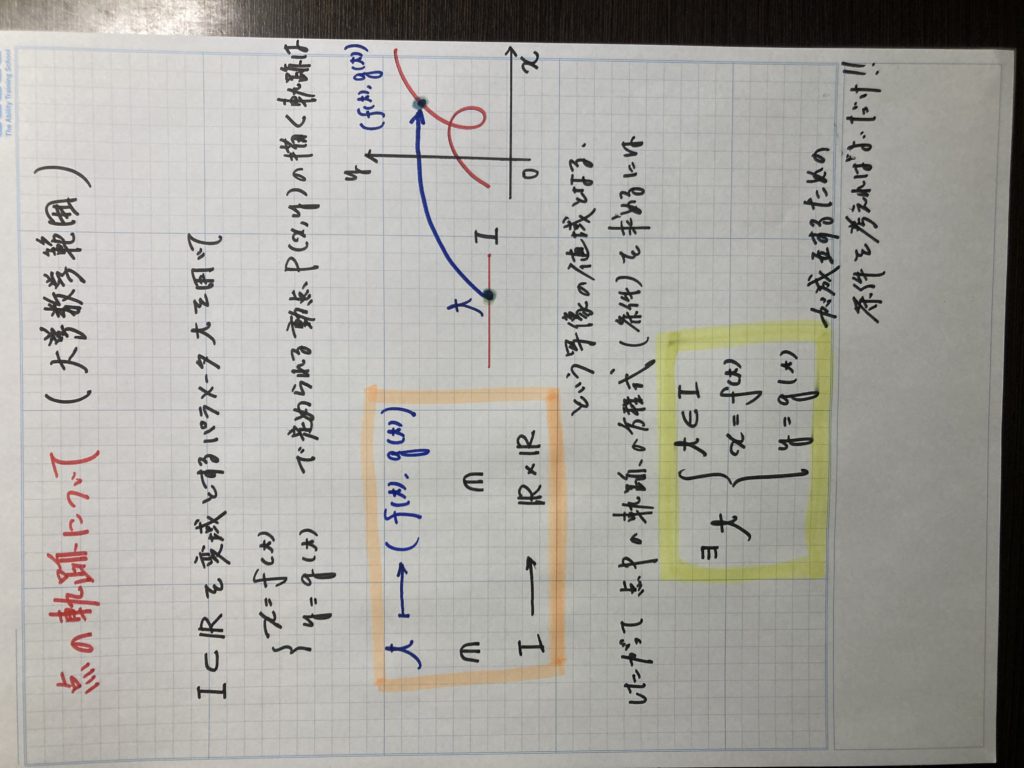
つまり・・・・彼らの、モヤモヤを払しょくするには、

これを教えるのが一番ということです!!

点の軌跡　=    存在条件　　そのもの!!

 

北嶺生であれば、たとえ中3生であっても、大学数学には食いついてきます!!

それだけ、知的好奇心は旺盛ということ!!

 

 

北嶺生が、望んでるモノは・・・・

 

難しいコトよりも、本質論!!

 

 

 

 

本日も、最後まで、読んでいただき、ありがとうございました。