例えば『連立方程式』・・・・・・

中学でも学習しますし、高校でも学習します。

一体、何が違うんでしょうか?・・・・・・

 

まず、中学で学習する連立方程式は・・・

◆

 

◆では、高校で学習する連立方程式は?

◆

◆

 

 

一体、どこが違うんでしょうか??????

 

 

同じ『数学』なんです!!

しかし、中学数学と高校数学は、別物!!・・・・・こう考えた方がいいです。

確かに、中学数学をベースとして高校数学はあるんですが・・・・

 

中学数学と高校数学の決定的な違いを分かり易く書けば・・・・

【中学数学】

『わかる』= 『できる』

『問題を解く』＝『作業』

 

【高校数学】

『わかる』　≠　『できる』

『わかる』⇒　『反復』　⇒　『できる』

『問題を解く』＝　『知的格闘』

 

 

高校数学では、『わかる』と『できる』は、全くの別物であり、

両者の間には、大きな壁が存在してます!!

高校数学では、『問題を解く』とは、試行錯誤の連続、すなわち『知的格闘』そのもの。

作業として、解けるのは、教科書の例題、練習問題レベルのみ。

 

もう少し踏み込みます。『連立方程式』を例にします。

 

中学の連立方程式は、解を求めることが出来る・・・ここがゴールです。

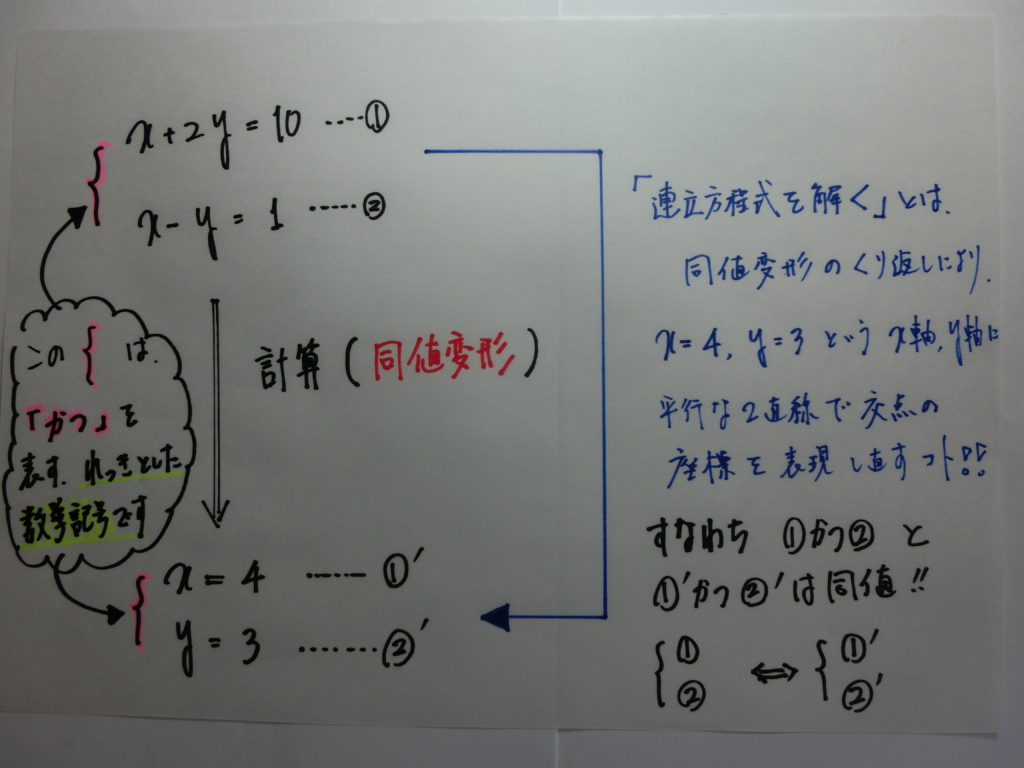
高校の連立方程式は、同値変形の概念を理解することが、ゴールなんです。

すなわち、連立方程式を題材にして”同値変形”を学ぶんです!!

この考え方をベースとして軌跡、通過領域、存在範囲へと進んでいくわけです!!

 

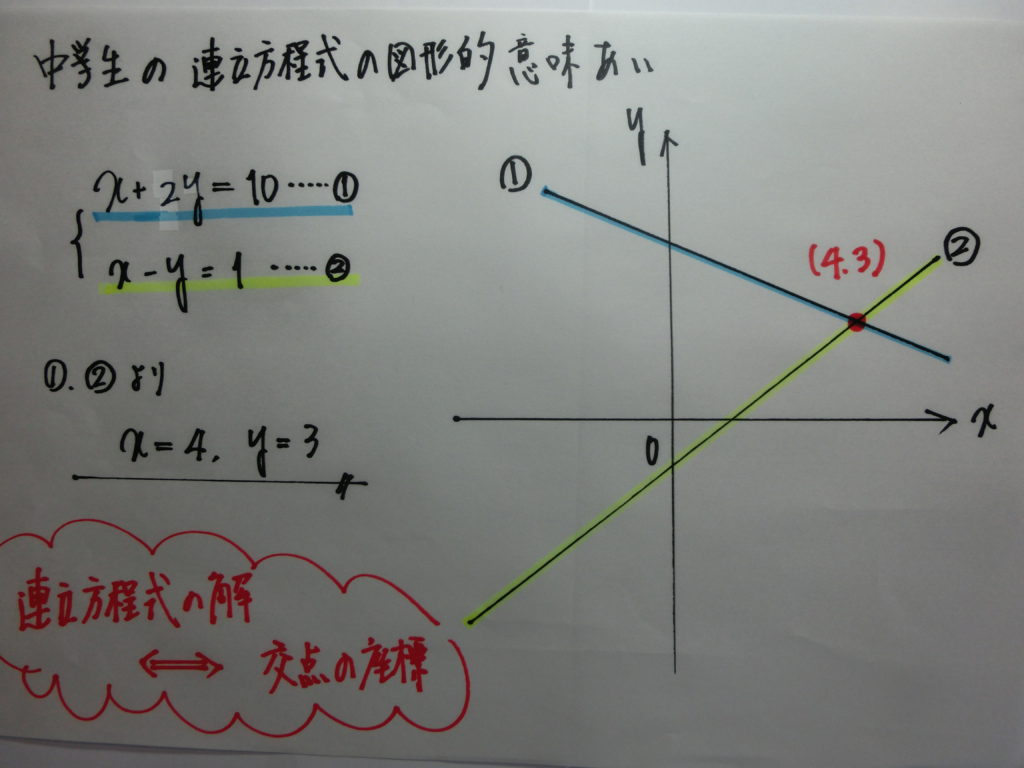
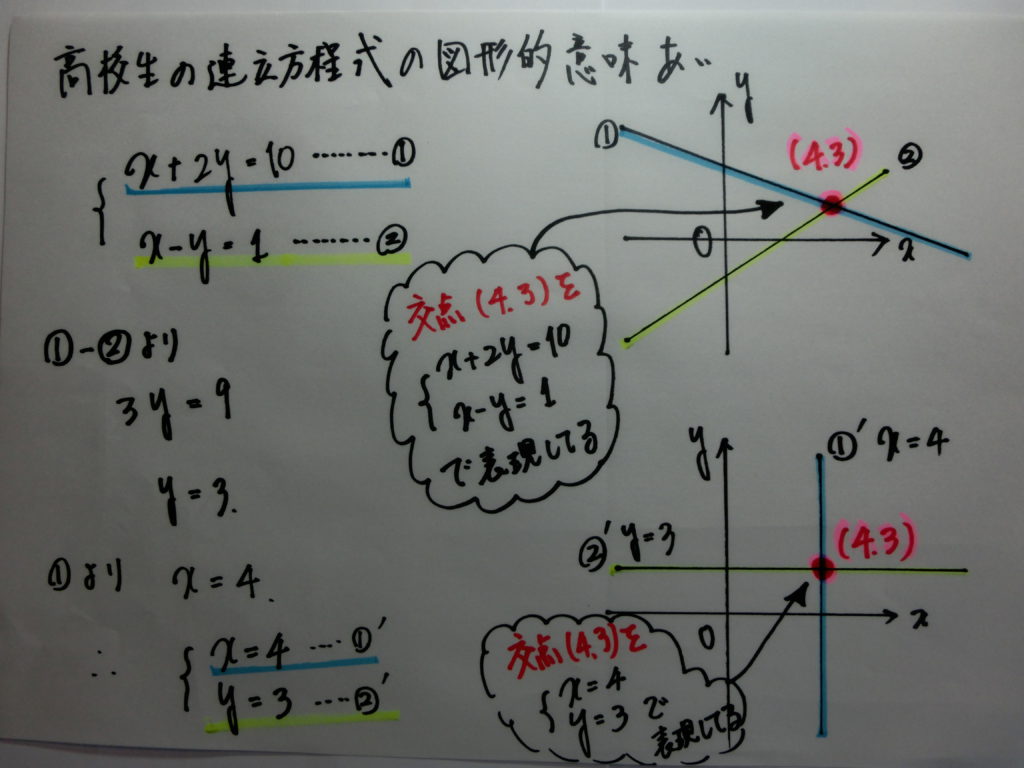
更に言えば・・・・連立方程式の図形的意味合いについて・・・

中学では、連立方程式の解　⇔　交点の座標

高校では、2直線の交点の座標の表現の仕方を　最もシンプルな2直線で表現し直す

 

こういうことです!!

 

ところが・・・・・連立方程式なんて中学でやったし楽勝～・・・

で終わらせてる高校生が多いんです(泣)・・・

 

解けるから大丈夫・・・・・という中学数学の感覚から脱却できてないんです・・・・・

 

こういった生徒は、やがて、『解法丸暗記』・・・・・・

暗記した解法を再現するだけの勉強になっていきます・・・・・・・

 

まとめます!!

中学数学　⇒　作業中心

高校数学　⇒　論理的思考中心

 

さらに・・・・やっかいなことに、この違いを認識できないまま、

中学数学の感覚で、高校数学を勉強しようとしてる生徒が相当数いるって事です。

 

 

実力養成会の現高1の会員のほとんどは、高校入試終了直後から、

本格的に高校の勉強をスタートさせてます。

私もバリバリ指導させてもらってました!!

数学は、もちろんのこと、それ以上に意識してたのは、

自学自習のスピリッツを叩き込む!!  ということだったんです!!

 

ですから、今回の定期考査で高1生がメチャクチャ結果をだしてるのは、

私からすると、当然の事・・・・・といううとらえです。

逆に、あれだけの結果をださないと、保護者の方に顔向けできません(笑)

 

なぜならば・・・・・・他の生徒が、入試が終わって遊んでる中、

我々は、あれだけのことをやってたんです。

 

 

 

今日も最後まで、読んでいただき、ありがとうございました。