高2『空間ベクトル』導入部の指導例を紹介させていただきます。

 

『空間ベクトル』を苦手とする生徒は多いです!!

 

それは、なぜか?

いたってシンプルな理由です。

 

『イメージする』ことが、下手だから・・・・

『イメージする』方法を、知らないから・・・

 

空間ベクトル・・・・・

カギは『図』を描けるか、どうか?・・・・極論するとココに帰着します。

 

ですから、私は、空間ベクトル指導の際は、とにかく、『図』を多用します!!

『このようにして、図をドンドン描いていくこと!!』を強く言い続けてます!!

とにかく、図を多用し、図とにらめっこする事!!・・・・ここを強調します!!

生徒にとって、『図』は、最初から与えられるモノ・・・・こう考えがちです。

『図』は、自分で描くもの。

『図』が、羅針盤となるんです。

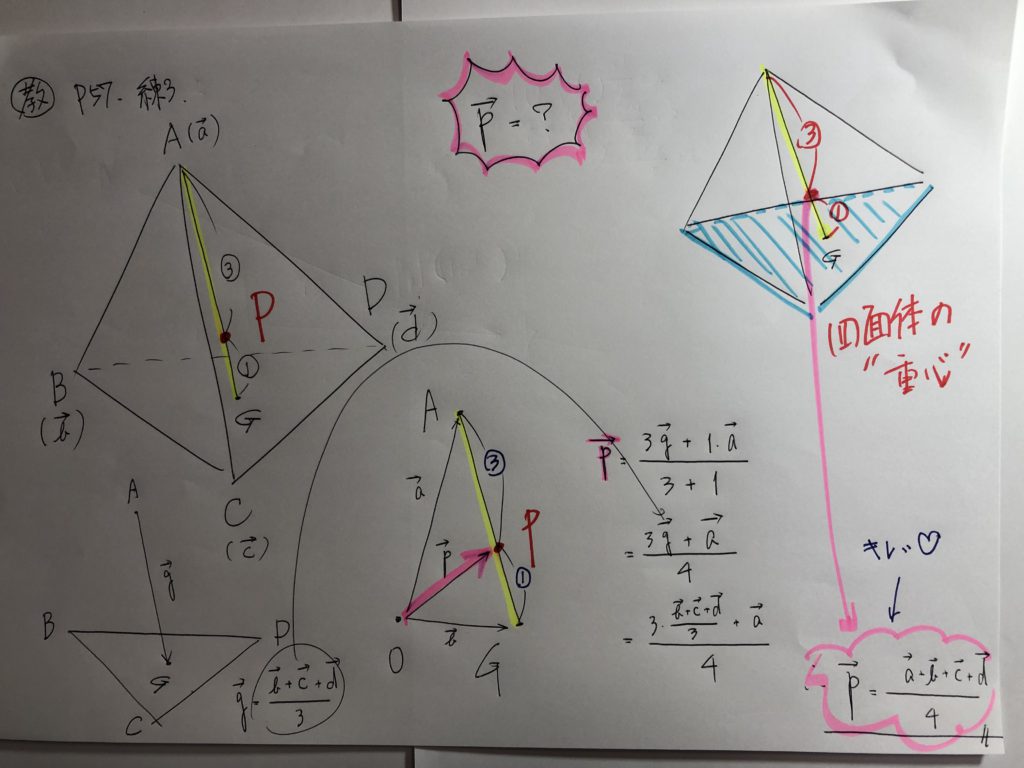
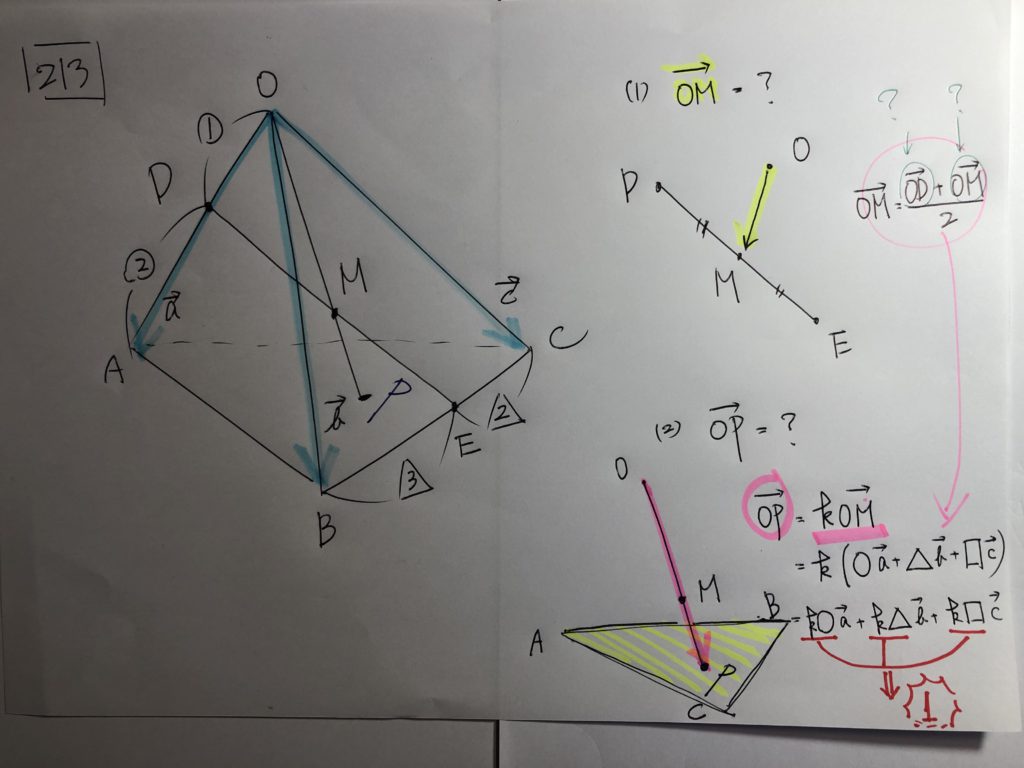
こういう”感覚”が身に付いてくると、生徒のノートは、おのずと、

こういう感じになっていきます!!

 

空間ベクトル・・・・・『図を多用!!』の他にも大切なことがあります!!

 

それは・・・・

教科書に書かれてある、”当たり前のこと”　に対しても、疑問を持つこと!!

 

なんで?

 

どうして?

 

の疑いの目を持つこと!!

 

そして、その疑問に対して、明確に答えられるようになること!!

 

これが、私がよく言う”基本”です!!

教科書に書かれてある事は、”基本”ではないのです。

教科書に書かれてある事は、”初歩”です。

 

 

例えば・・・・

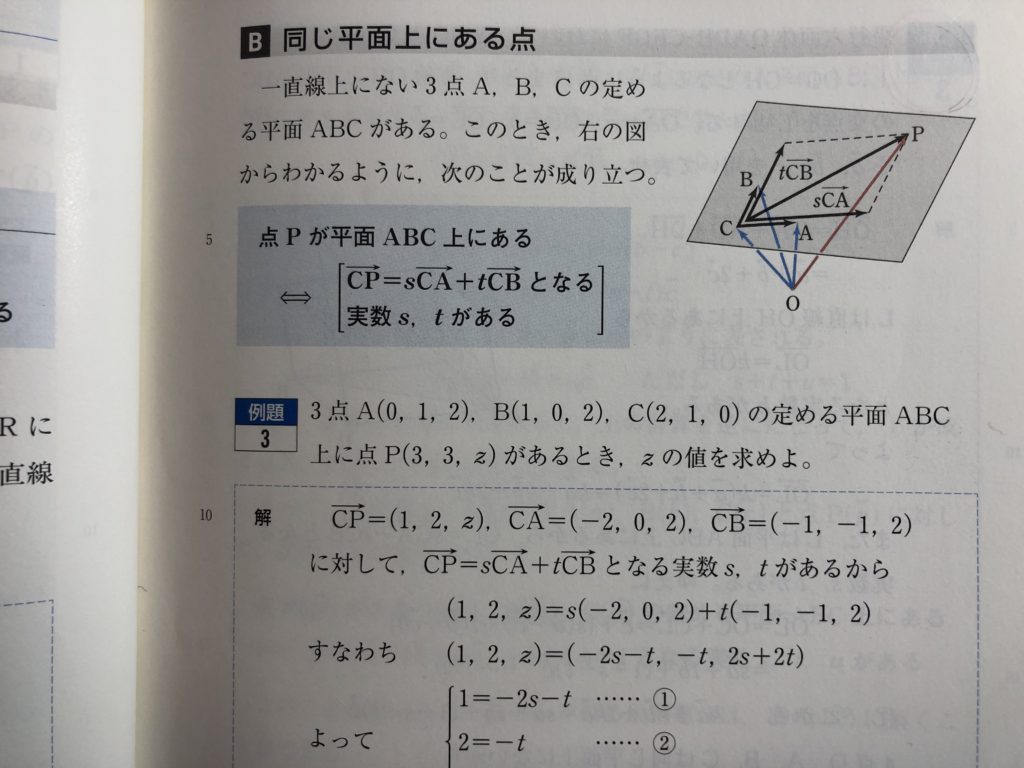
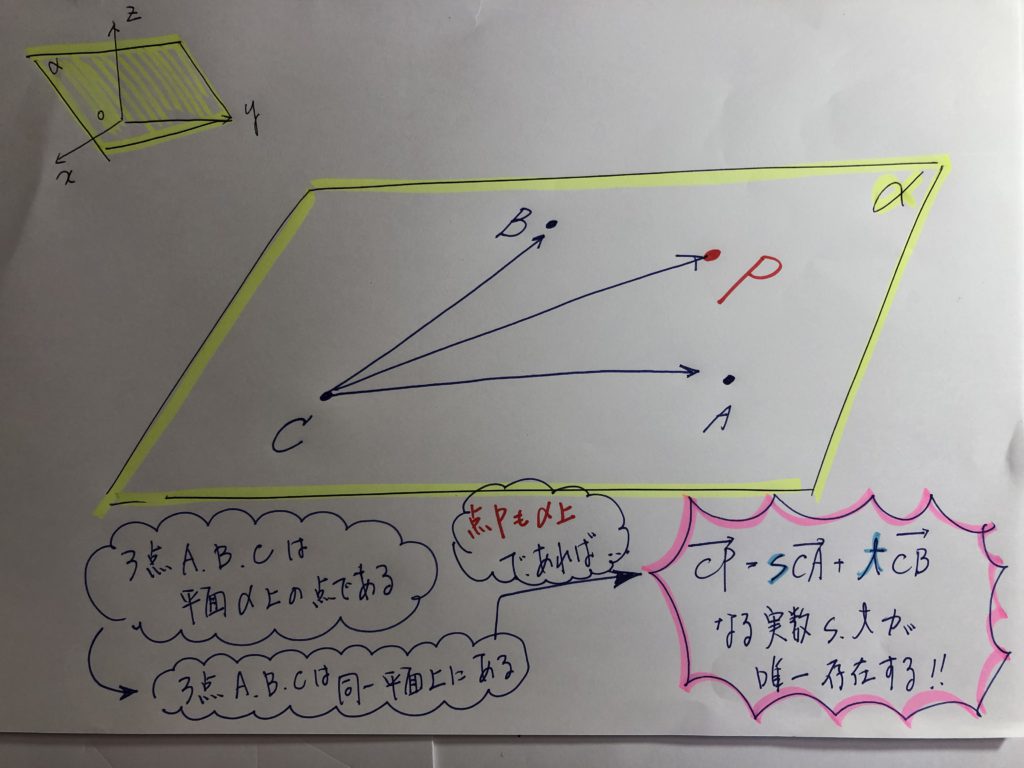
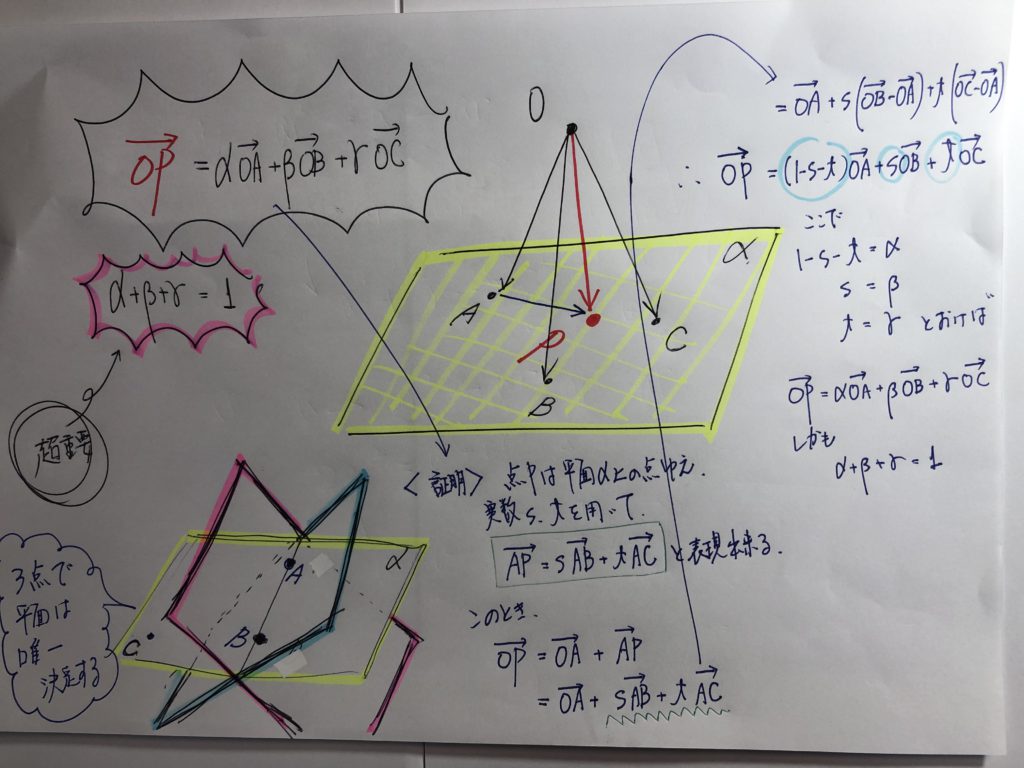
どの教科書にも、書かれてある、下の画像!!

なんで?

どうして?

皆さんは、この問いに明確に答えられますか?

 

◆

◆なぜ?・・・・どうして?・・・・その疑問に明確に答えられる”ロジック”を構築するこ

とが、基本です!!

 

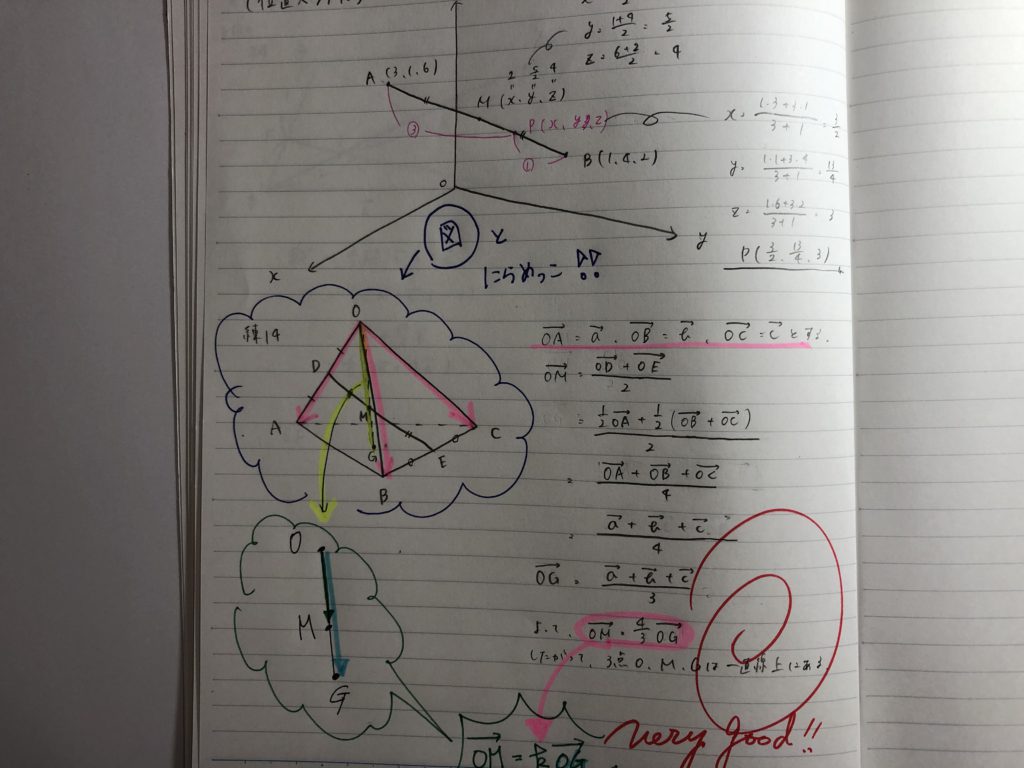
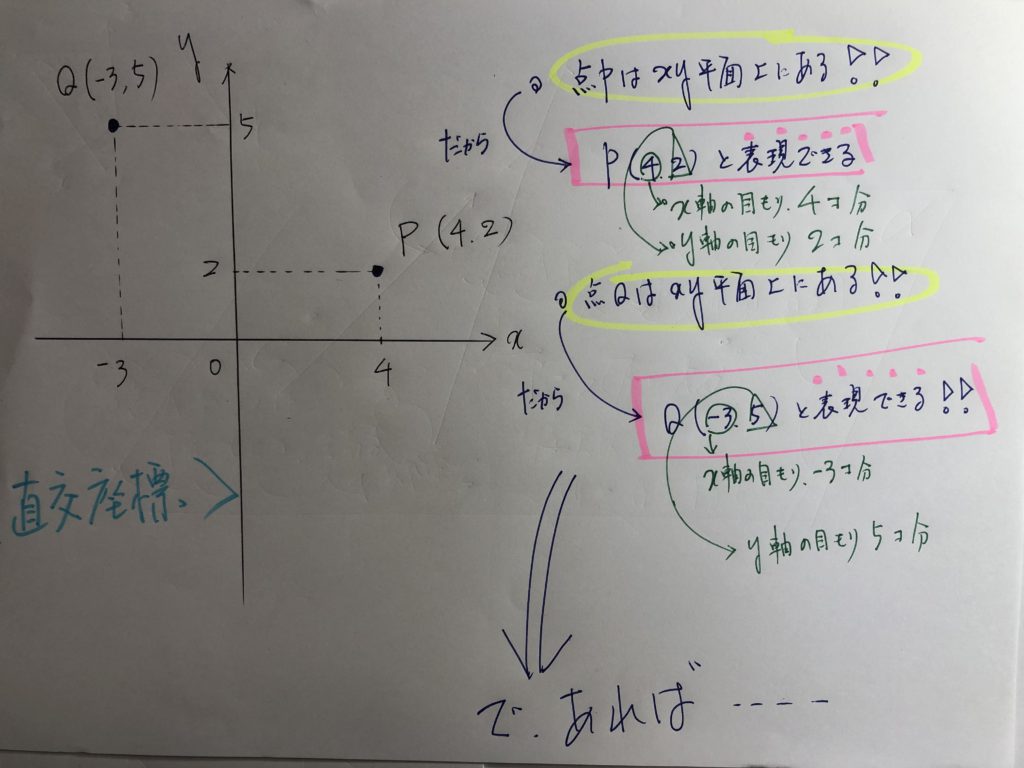
まず、直交座標の話から入ります。

斜交座標へと話を膨らませていきます!!

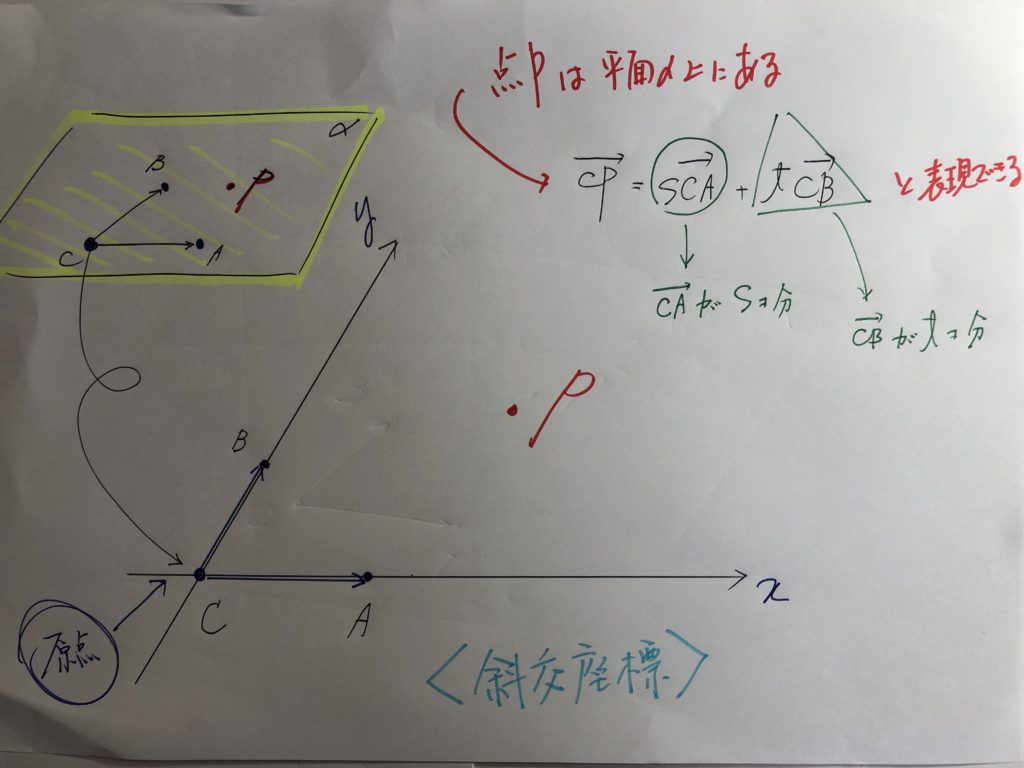
以下のように、説明すると・・・・

生徒は、ストンって”納得”・・・・いわゆる“ふ”に落ちるってやつです・・・・

このことをしっかりと理解できれば、『共面条件』関連の問題は、ほとんど、対応可能

となります!!・・・・・・なぜならば、『根底』が理解できてるから!!

 

当たり前のことに対して、疑問を持つ・・・・自問自答する。

自分なりに、納得のいく説明ができるようになる。

これが、『基本』です。

 

例えば・・・・・・

分数の割り算。

『ひっくり返して、かける!!』

なぜ?

どうして?

理屈がどうであれ、ミスなく計算できればOKでした。

しかし、高校数学は、高度になればなる程、理屈を根底から知らなくては、

対応出来ません!!

 

『理屈』を知ること、理解し、納得すること、そして自分自身に対して納得のいく説明

ができること・・・・これが『基本』です!!

 

 

 

『基本』と『初歩』は、全くの別物です。

 

 

今日も、最後まで、読んでいただきありがとうございました。