空間ベクトル・・・・一口で言っても、様々な問題がありますが、
パラメーター表示系の問題を除けば、
次の、九大の過去問、とても重厚感のある良問といえます。
これが“空間べクトルのゴールの問題”と言ってもいいのではないかと思ってます。
細かいことですが・・・・・とても大切な部分です!!
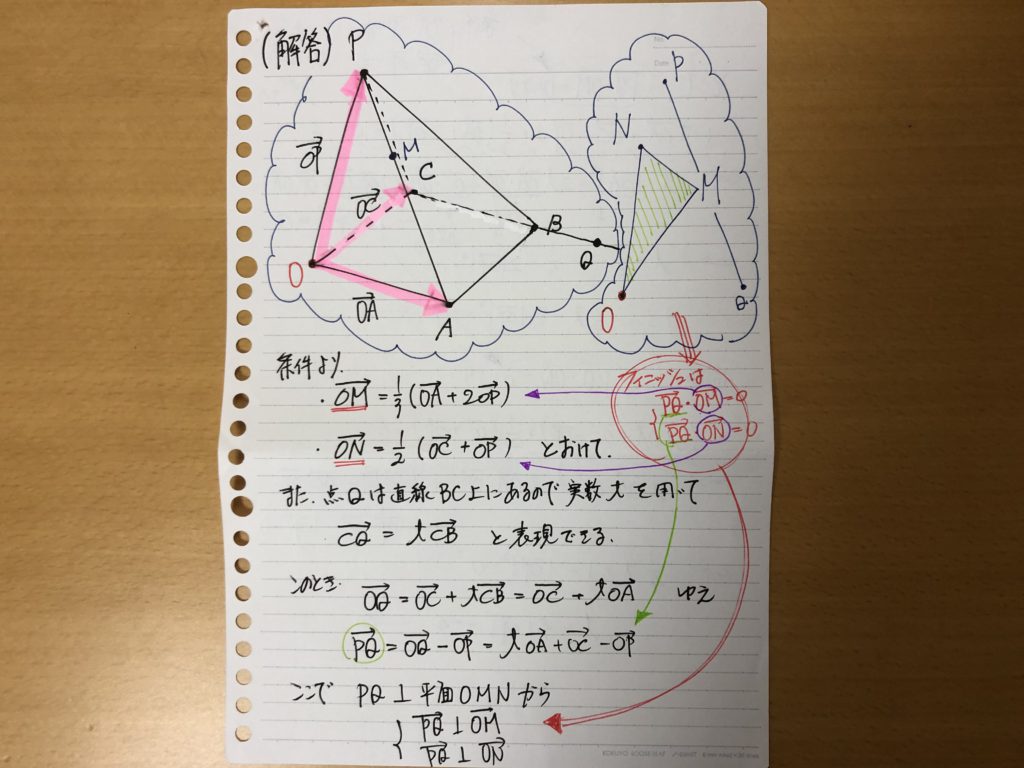
『正方形OABC』となってますね?・・・・・『正方形ABCD』でない理由は?
作問者は、頂点Oを原点とする座標空間で考えてね!! というメッセージですからね!!
ですから・・・・
フィニッシュは、OAベクトル、OCベクトル、OPベクトルの3つのベクトルですべて表現
して、内積ゼロ・・・・・・方針というか見通しは立つんですが・・・・・
ただし・・・・底面が正方形です!!
ってことは・・・・OAベクトルとCBベクトルは、『イコール』です!!
地味に、ここに気付けないと、フィニッシュに持っていけない!! こういう事です。
どうやら、問題を解くカギというか、”決定的ポイント”は、以外にも
OAベクトル = CBベクトル と出来るかどうか?・・・・ここです!!
この問題をある生徒に演習させました!!
PQ と平面OMNが垂直 ⇔ PQベクトルとOMベクトル、ONベクトルの内積ゼロ!!
連立です!!
未知数2つです!!・・・・・それは、置いた t と・・・OPベクトルの絶対値の2つ!!
◆
◆
本日も、最後まで、読んでいただき、ありがとうございました。