三角関数は、典型的な周期関数であり、実に調和のとれた性質を持つ。

それゆえ、周期的な現象・・・・・例えば、地球の公転・自転、人間の脈拍、

音、光や電波の伝幡を解析するためにはなくてはならないモノだ。

 

さて・・・・

数Ⅱで学習する『三角関数』

まさに公式のオンパレードと言える!!

そもそも、加法定理とは、関数 f(χ＋y) をf(χ)やf(y)を用いて表す公式を言う。

 

sinχ、cosχ　については、単独では簡単な加法定理は存在しない。

しかし・・・”組”としての加法定理は成り立つ。

すなわち、sin(χ＋y)、cos(χ＋y) をsinχ、cosχ、siny、cosy で表すことは可能だ。

 

『長いつきあい』となる基本公式だ。

 

 

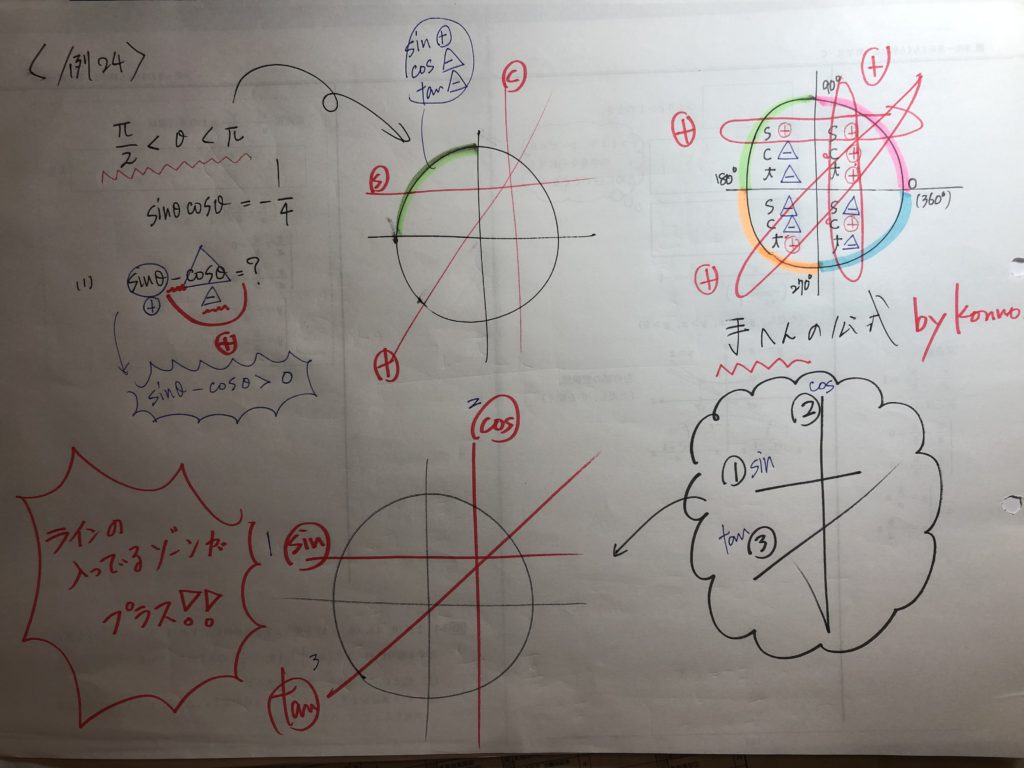
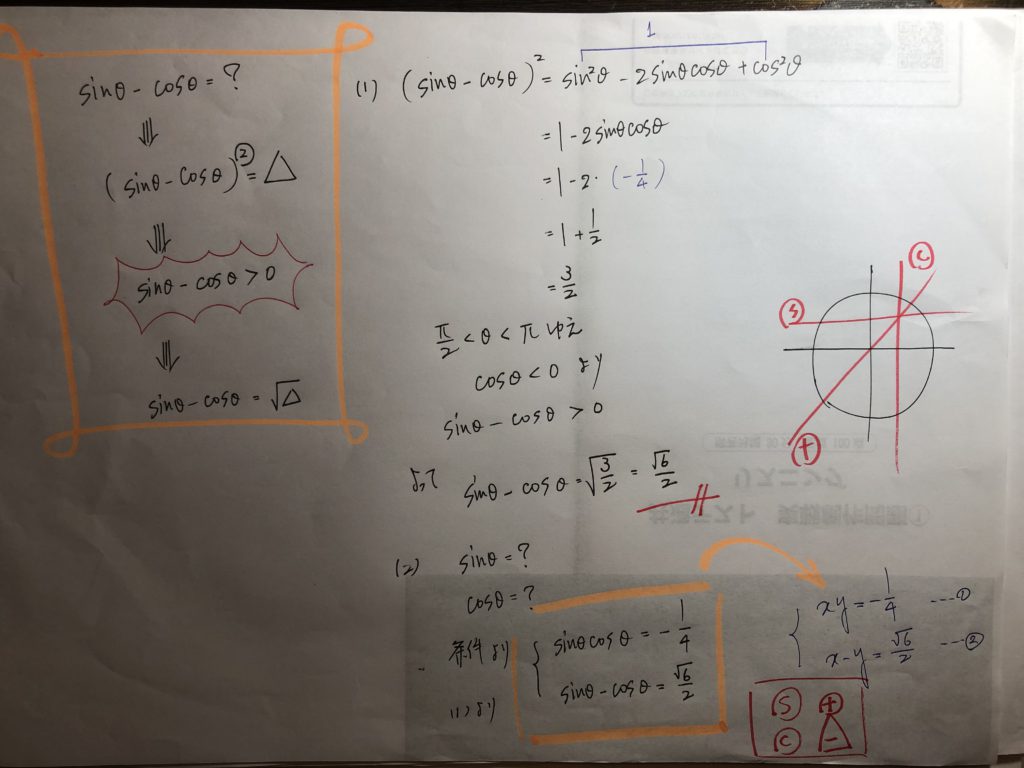
これら一連の公式は『その場で導くもの!!』

 

 

時には、図を描きながら・・・・

時には、理屈を考えながら、

 

 

その場で導く!!

 

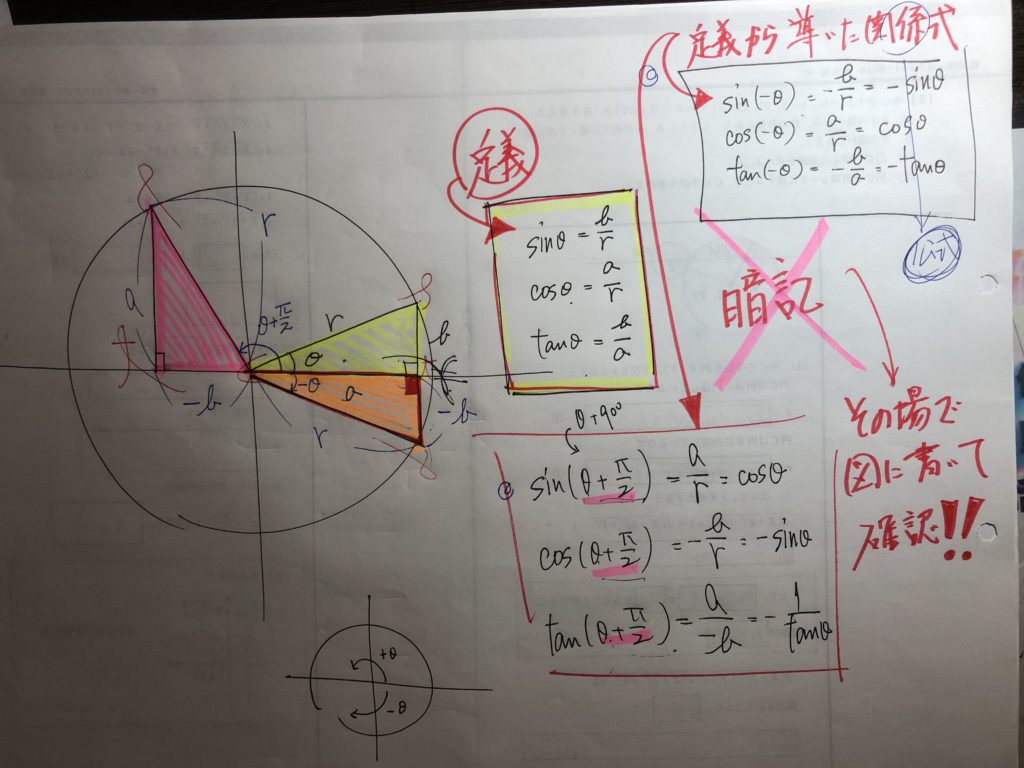
定義より導かれた関係式・・・・これが公式!!

あくまでも、公式とは、結果を切り取ったモノ。

 

 

 

複雑に見える公式群であるが、無理して覚える必要は一切ない!!

sin、cosの加法定理さえ正確に覚えていれば、たちまち導き出せる・・・・

 

 

 

本日も、最後まで、読んでいただき、ありがとうございました。