まず、問題は、これでした!!

 

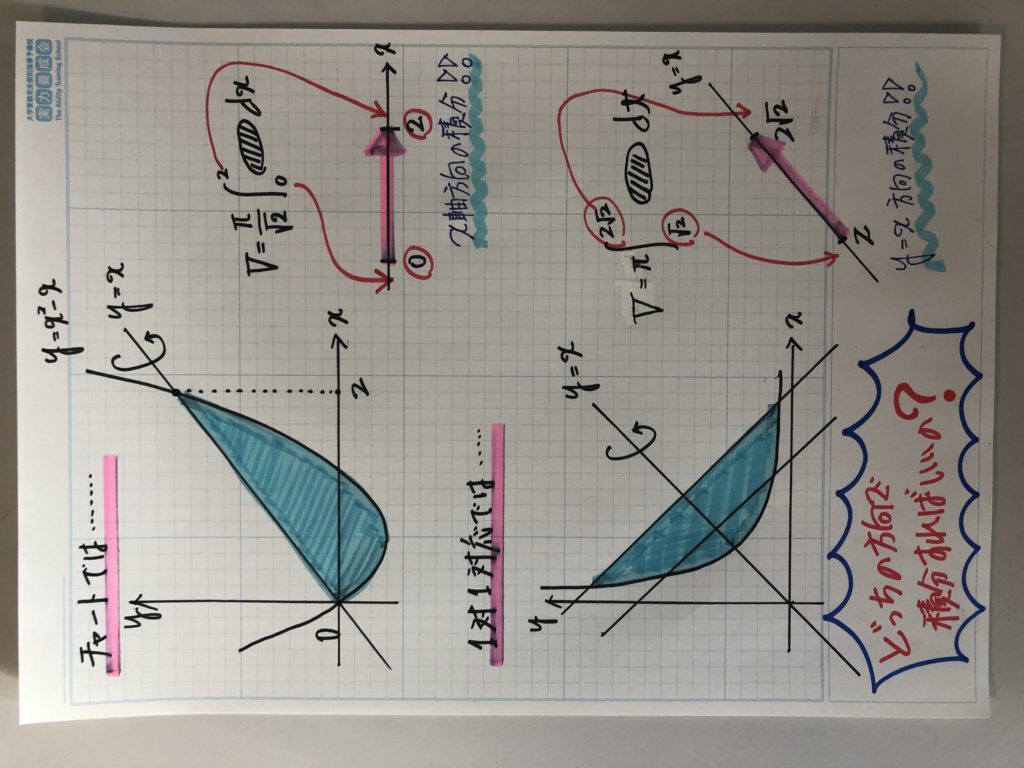
チャートより

 

1対1対応より

 

まず、生徒が、悩むところはズバリ、ここなんです!!

 

 

どっちの方向で積分すればいいの?

 

 

すなわち・・・・

チャートと1対1対応・・・・積分方向が異なります。

このように、その問題集、参考書等で積分方向が異なるため、

生徒が混乱します!!

 

 

結論は、どっちでもOK!!　計算がラクな方で!!

 

 

しかし・・・・生徒にとっては、どっちが楽?　すらも分からない・・・

こんな感じなんです!!

 

 

そもそも、体積を求めるときの、本質とは?

 

ボンレスハムとペラペラハムの関係でしたね。

 

ボンレスハムの体積を求めるときは、

超薄くスライスされたペラペラハムの面積を考え、

それを積分(寄せ集めてまとめる)することで体積を求めることが出来る!!

 

ですから・・・・・

積分する方向(寄せ集める方向)が異なるだけの話で、

本質は、何も変わらない!!

 

こういうことです!!

 

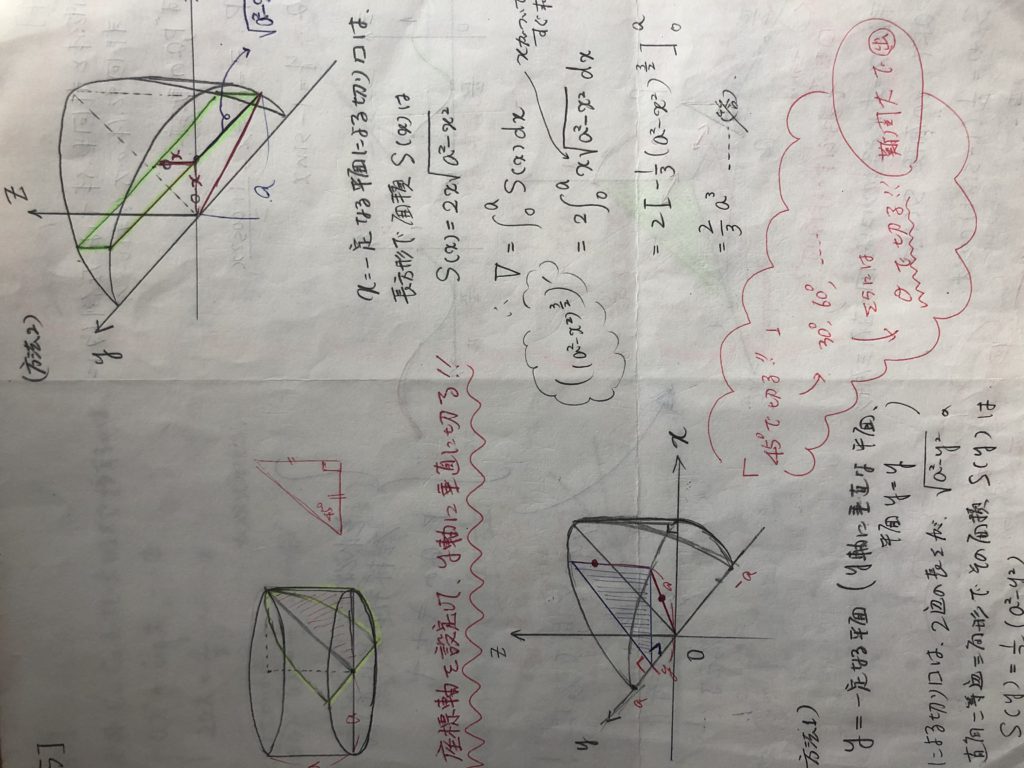
例えば、ある立体の体積を求めるとき、

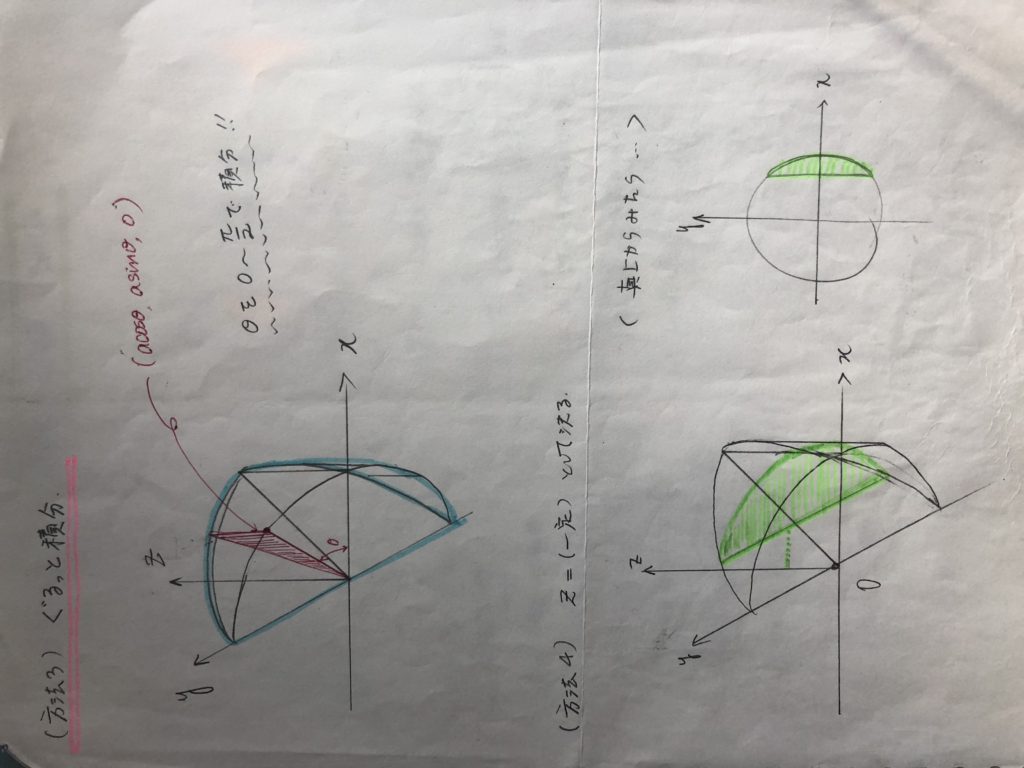
χ軸方向、y軸方向、z軸方向、もしくは、原点の周り方向、

どの方向で積分しても、しっかりと原則通りやれば、体積は求まるのです!!

 

しっかりと《原則通り》やれば、体積は求まります!!

 

斜軸回転でも《原則》は変わりません!!

 

この《原則》こそが、私がいつも言ってる『本質』です!!

 

問題の見た目の難しさに気をとらわれ、

『本質』が、ないがしろにされてるんです!!

 

生徒が、この斜軸回転体の体積を苦手とする原因は、ここにあるんです!!

 

では・・・・・《本質》とは?

 

それは、企業秘密とさせてください!!

 

 

ちなみに・・・・・

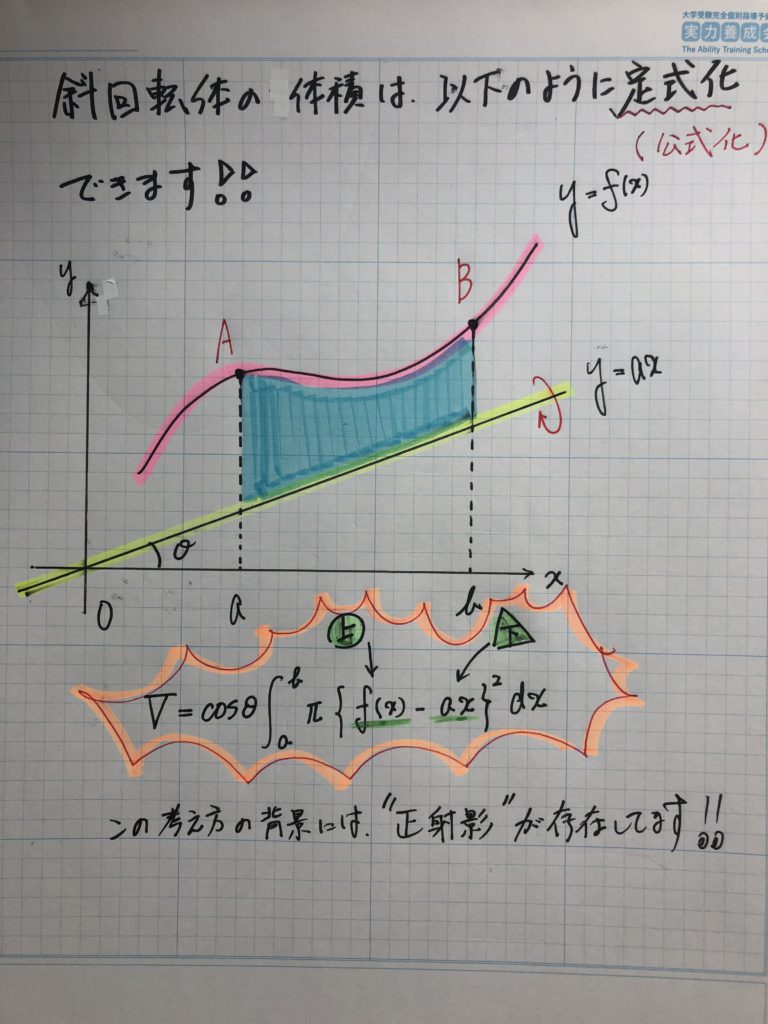
この斜回転体の体積を求めるとき、

キレイな一発公式が存在します!!

 

 

この公式に便乗すると・・・・瞬殺です!!

一応紹介しておきます!!

 

本日も、最後まで、読んでいただき、ありがとうございました。