グラフを追跡(描く)ときの正しい態度について!!
割と複雑な関数が与えられ、グラフの概形を知らなければならない時、
何が何でも微分して増減表を作る受験生をよく見かけます。
ハッキリ言って・・・・・とても”損”なやり方です。
微分が有効なのは、局所部分の増減やグラフの凹凸を調べる場合です!!
ですから・・・・・
①グラフの概形をつかむ!!
それから・・・
②細かい部分を追跡する!!
これが・・・・ただしい態度です!!
とは言え・・・・①の段階で、何をやったらいいのか? わからない・・・
というヒトもいるでしょう・・・・
“ありがちな抽象論”ではなく、具体的に書かせてもらいます!!
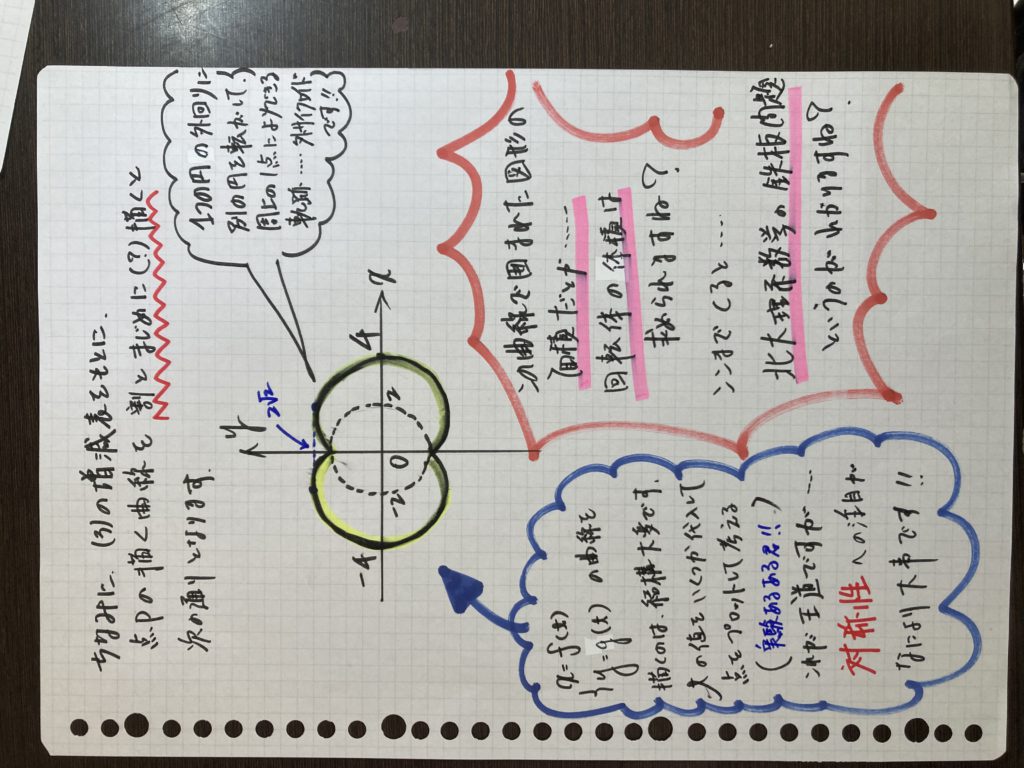
この問題は、最終的に点Pの描く曲線の長さを求めたい!! こういう問題です!!
グラフの概形がつかめれば、グラフの対称性に着目すると簡単に求まります!!
いずれにせよ、(3)で最大値を求めるわけですから増減表を書かなければなりません。
私が皆さんに、声を大にして言いたいことは・・・・
式の形に敏感になれっ!!
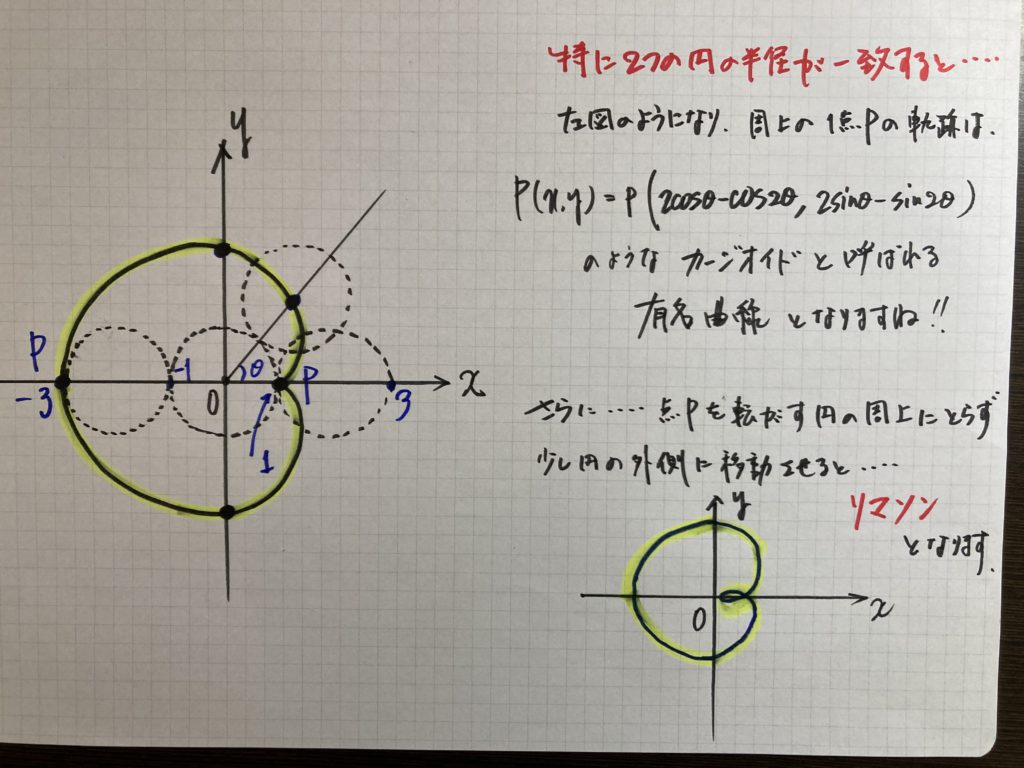
さらに・・・・話を膨らませましょう・・・
本日も、最後まで、読んでいただきありがとうございました。