札幌南1年生です、実力テスト対策の指導例です。

この日は『実力テスト対策』として、次の2題を深掘りしました!!

それにしても・・・・1年前はまだ中3生、でっ1年後に、こうして北大の問題に積極的に

取り組んでます、もはや、中学の塾の先生も解けないレベルの問題です。

この1年間の『成長・進化』に驚かされます。

通称『実テ』はほとんどが難関大の入試問題です。

そう、簡単には解けません。

こういった問題とどう向き合うのか?

やはり・・・・『感即動』です。

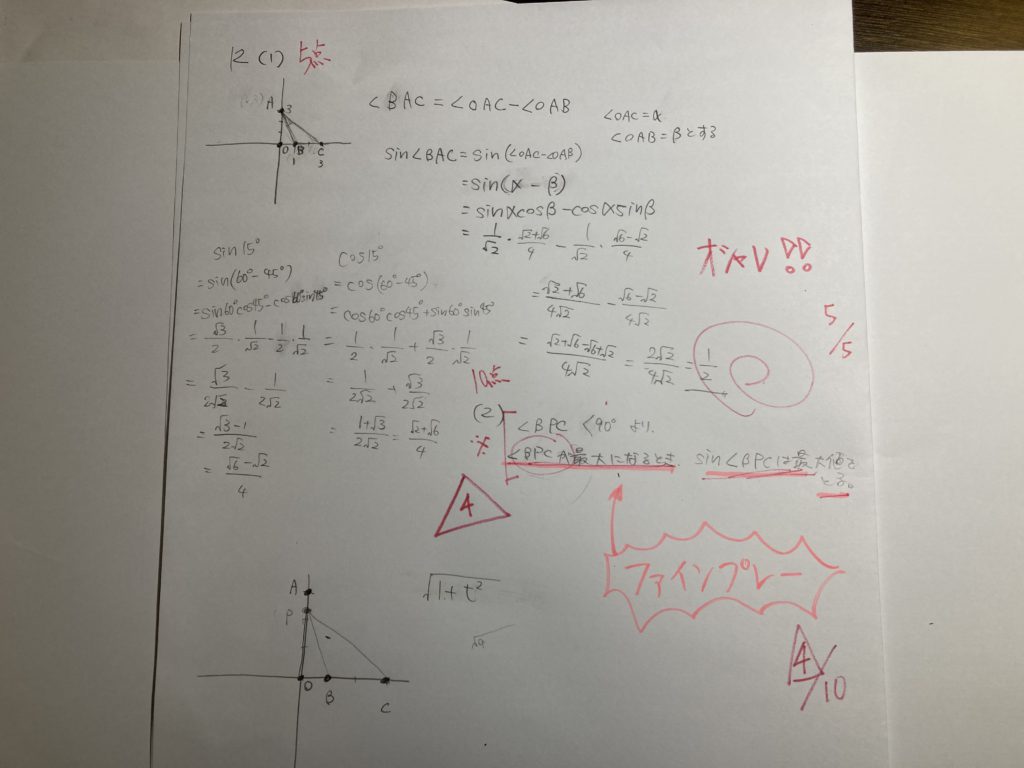
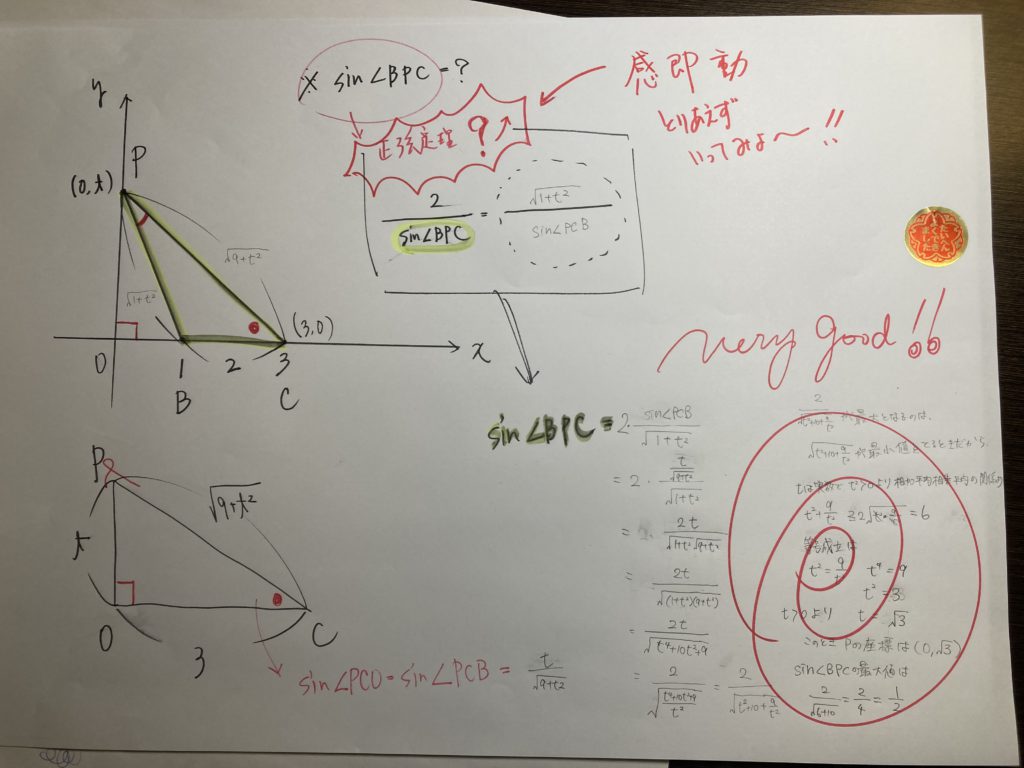
図のように、三角形と動点が与えられて、sin の最大値を求めます!!

三角形・・・・sin・・・・と言えば? 『正弦定理』もしくは『余弦定理』

であれば・・・・sin を t で表現してみよう!!

こんな話です。

もちろん・・・・見切り発車で構わないのです!!

思ったら(行けそうなら)ます、手を動かすんです!!

『とりあえず』　で全然いいのです。

手を動かしていくうちに、ドンドン、点と点がつながっていきます・・・・

でっ・・・・思ってもみなかった状況(相加相乗平均の関係に帰着)に遭遇します!!

結果として・・・・えっ!? 解けたぁ～!! となります。

中学時代から、手取り、足取り　一から十まで、すべてお膳立てされた中で、問題を解い

てきた生徒は、こういった類の問題は、手も足も出ません。

中学時代に染み付いた“他力本願”な学習姿勢は、そうそう簡単には払拭出来ません。

トップ高へ進学し『成績深海魚』になってる生徒の大半は、こういったタイプです。

本日も、最後まで、読んでいただき、ありがとうございました。