立命館慶祥高、高2生(一貫生)の指導例です。
数Ⅲ極限(連続性)の指導です。
まだまだ・・・・理解が”浅い”ということが、この答案から見えてきます・・・・
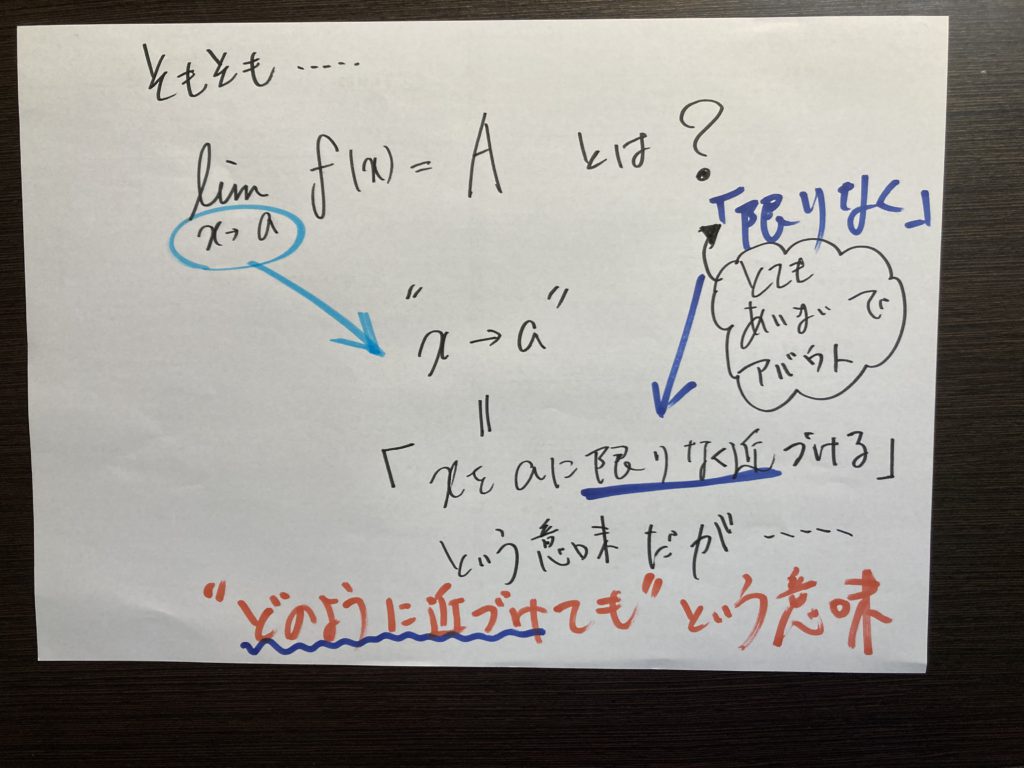
そもそも・・・・
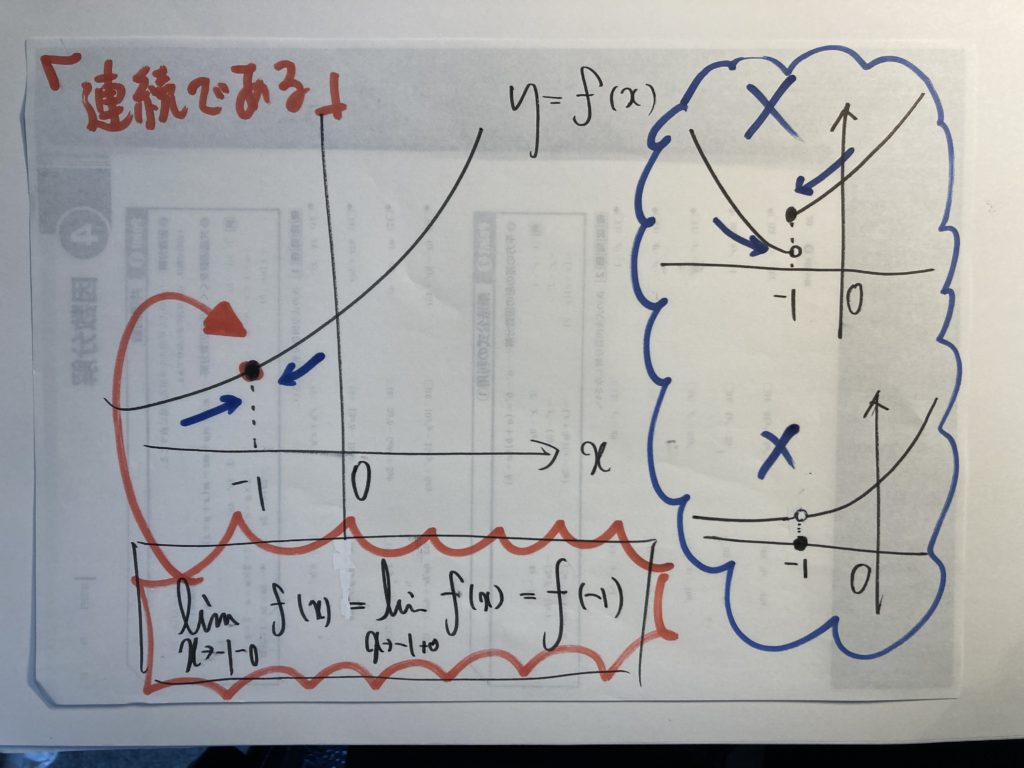
『関数 f(χ) が χ=a で連続である』とは?
つまり・・・・・『連続』の定義は?
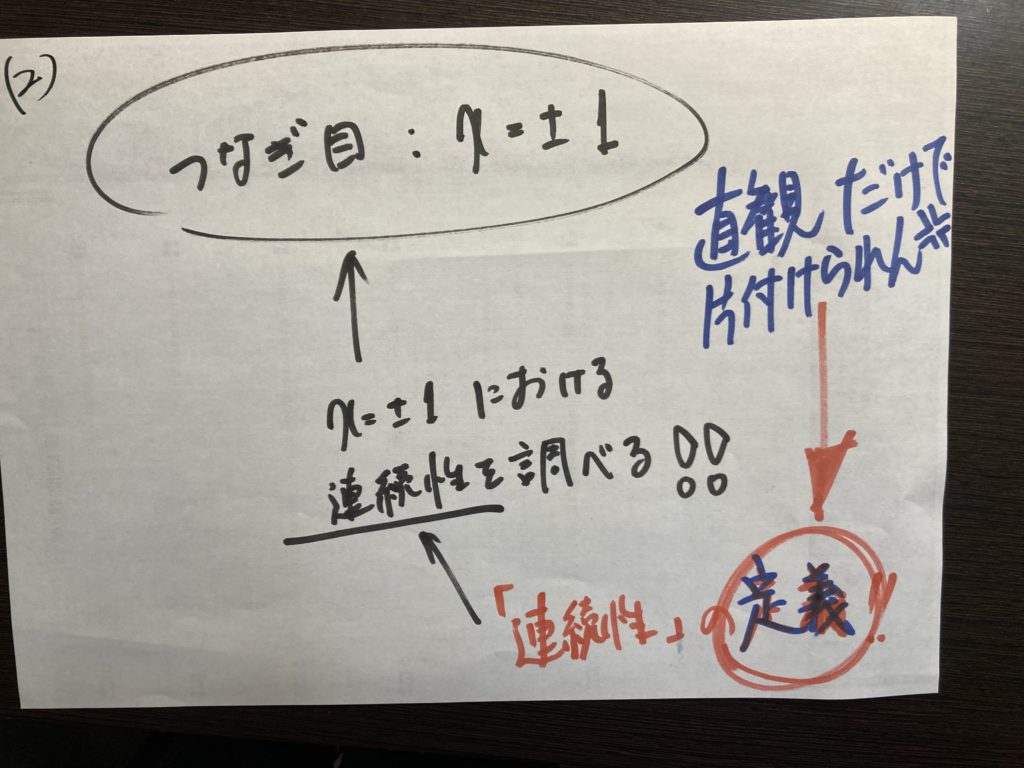
そこそこできる理系の生徒ですら ”直感”にゆだねて、感覚的に解こうとしがちです。
4step レベルなら、それなりに対応できます!!
しかし・・・・・難関大の入試にも十分対応しうる”強靭な足腰”にするためには、
極限の定義、定理に関して、”厳密さ” と”ち密さ” が絶対に必要です。
“直感”や”センス”だけで、片付けてはいけません!!
『解法パターン』だとか『公式』を意味も考えずに、マル暗記して、
それにあてはめて解く・・・・・・
“何も考えずに” “あてはめる” 一見すると効率的に思えますが、
ここが、諸悪の根源です。
大切なことは、自身を ”ごまかさず” 『なぜ?』を大切にすることです。
本日も、最後まで、読んでいただき、ありがとうございました。