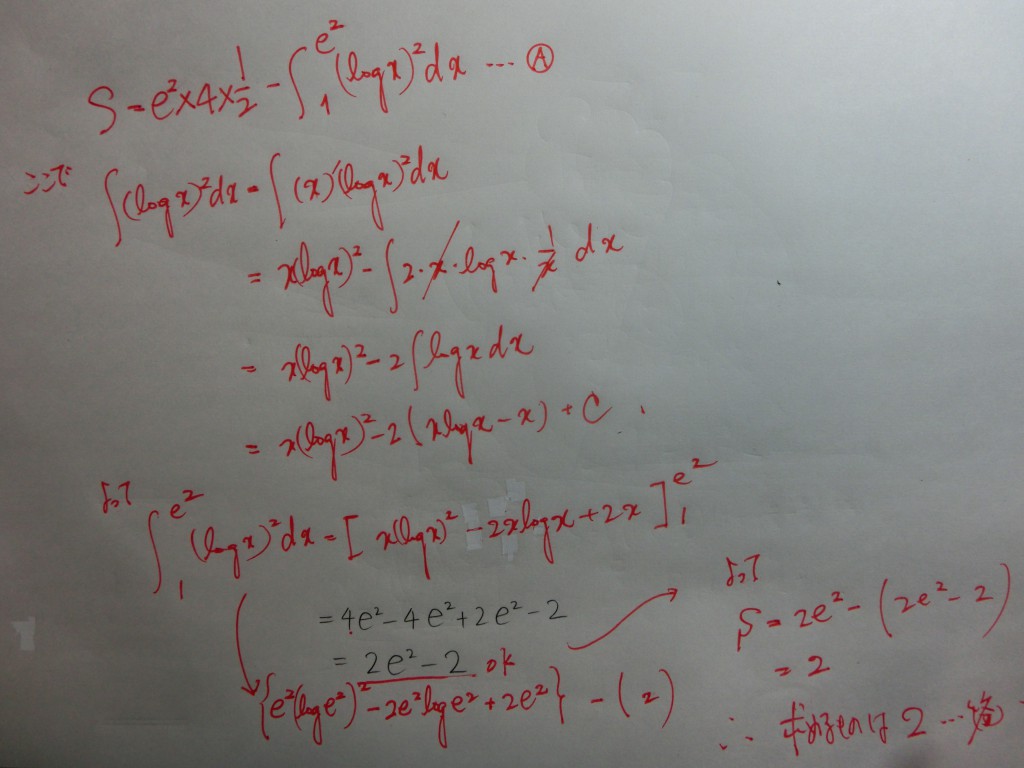理系数学を選択すると、微分・積分の学習を徹底的に強いられます。

 

この微分・積分という領域は、これまで学習してきた他の数学の領域とは、

一味も二味も異なります!!

 

なぜならば、そこには、『極限』を求めるという操作を通して、“無限”という概念が入

ってくるからです。

 

 

 

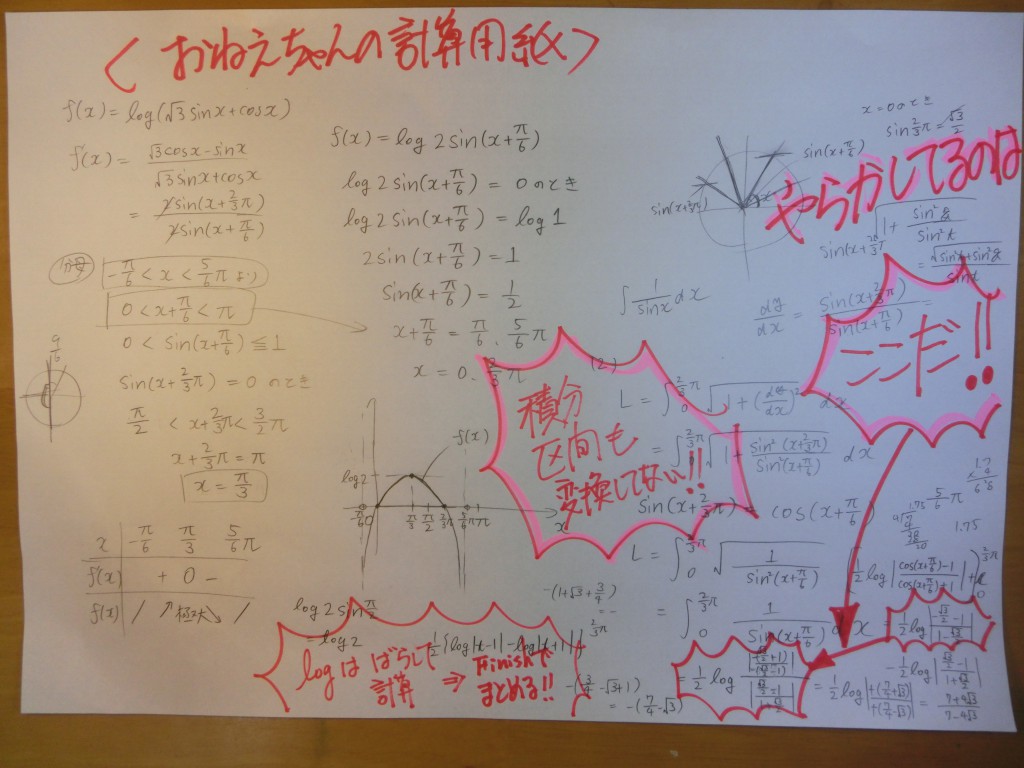
さらには、e のχ乗、　とか　logχ　とか　いかにも、扱いにくそうな　関数を相手にし

なければなりません。

 

 

そのため、初めて理系数学の微分を学ぶ者にとって、こんな問題に直面します。

 

①イメージがつかめないから、意味も分からないまま、式をいじくる。

②身近な興味を持てないため、どのような面白さがあるのかがわからない。

 

 

とは言え、教科書を理解し、パターン化された問題を反復練習する初期の段階では、

意味が分からなくても、興味がわかなくても、”根性” さえあれば、何とかなってしま

うのです。

 

さて・・・・問題は、この次です!!

 

学習の初期段階を経て、晴れて『考えて意味の分かる中級の微積分』に進もうとした時

、いかに、自分が、何も考えず、作業として計算してきたことに気付かされます。

微分することの意味を改めて考えさせられます。

 

勉強しているにもかかわらず、なぜか得点が伸びません。

勉強すればするほど、微積がわからなくなるのも、この時期です。

一種の壁にぶち当たるのです。

 

 

東西南北、旭丘に代表されるトップ高の2年生の理系の皆さんの半数は、

数Ⅲに突入しています。

まさに、これからが正念場になります!!

 

 

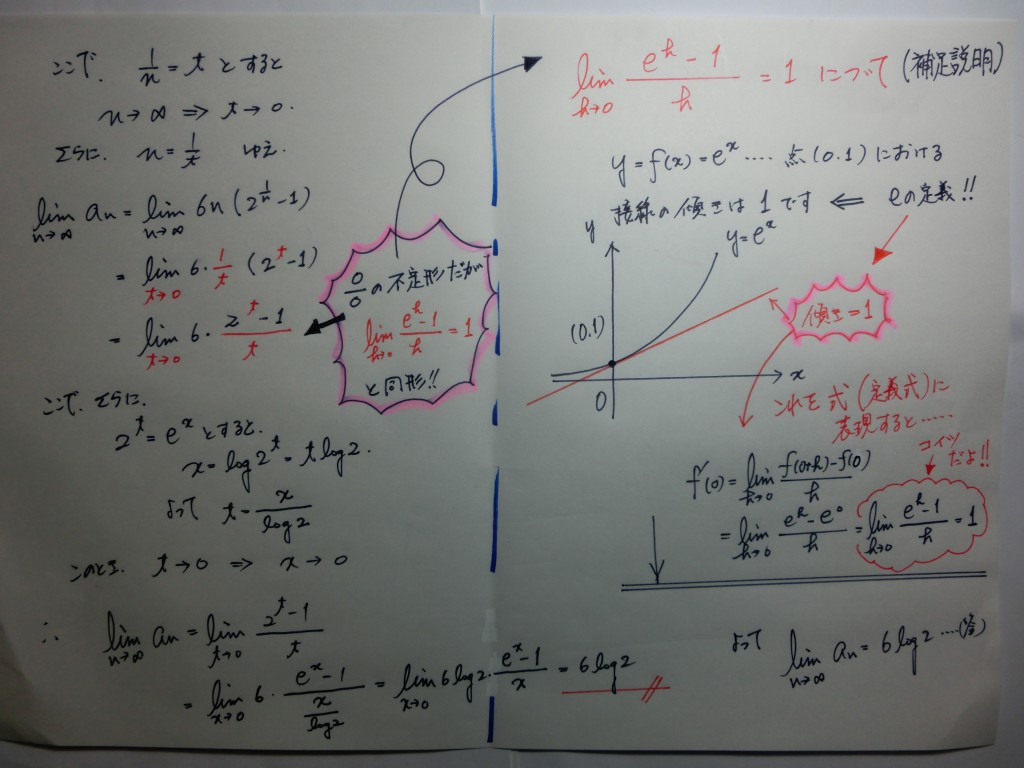
『そもそも、e って何?』

 

 

教科書に書かれてある”定義式”は、結果として導かれた、”同値式”　ですからね。

これは、基礎ではありません!!・・・・・あくまでも『初歩』です。

 

同値変形の連続・・・・その途中に現れる式をピックアップしただけに過ぎないのです。

では、同値変形　をする、一番の　”根っこ”　となる式って、何ですか?

 

ここを理解することが『基礎』です。

『基礎』とは、決して簡単なものではありません。

 

『e  って何か?』・・・・・・これに明確に答えられるようになれば、

 

微分・積分は意味の分かる身近な存在になります!!

 

そうすると・・・・

微分・積分はおそれるに足りません!!

やがて、微分・積分こそ得点源になっていきます!!

 

今日も、最後まで、読んでいただき、ありがとうございました。