第1回全統記述模試・・・・・全体的に難しかったですね。
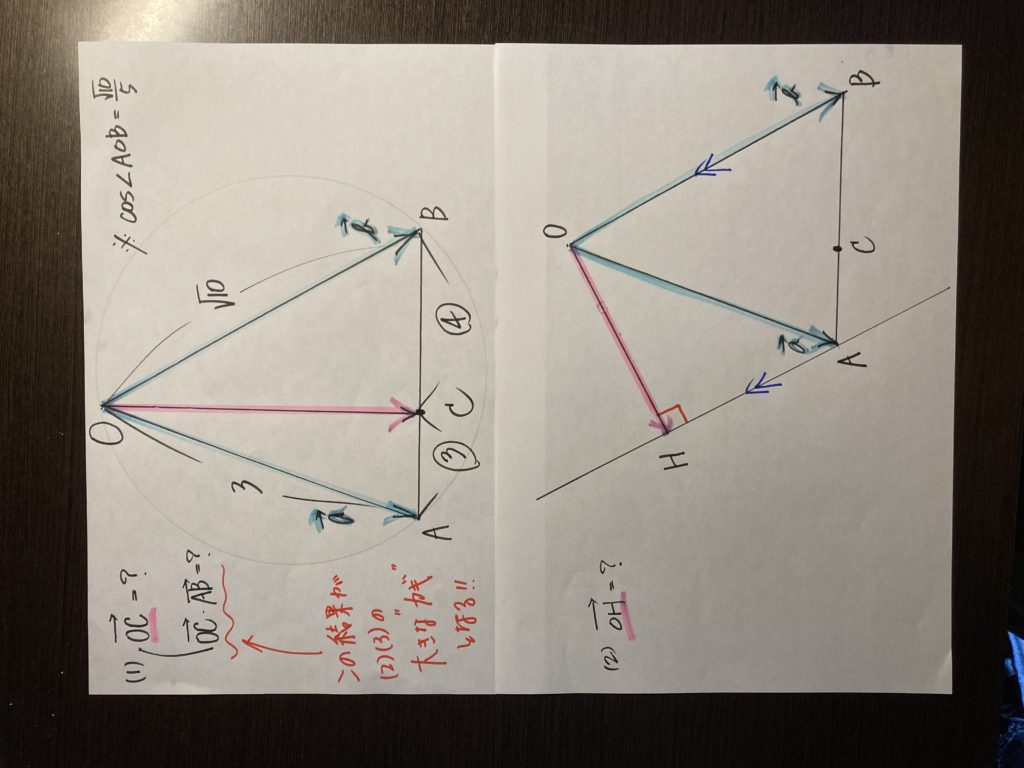
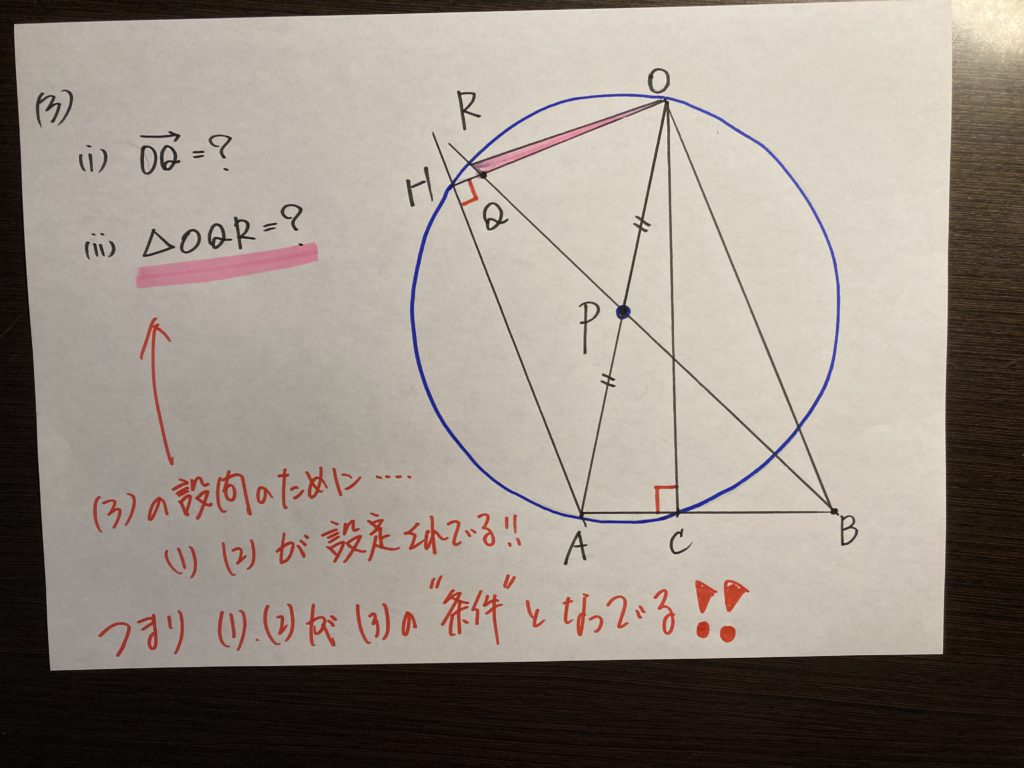
特に大問4番のベクトル、難しかったと思いますが、良問の極み!! と言えます。
みなさん・・・・どうだったでしょうか?
どこが・・・・・”良問の極みか?”
平面幾何の知識をフルに使いきって考える!!
つまり・・・作問者の意図がはっきりと主張されてる問題です!!
中学生が学ぶ、”有名定理”をふんだんに活用して解きます!!
これぞ、平面幾何の王道中の王道!! と言えます。
こういった”記述模試”の神髄は、作問の意図を見抜く力を養うことにあります。
それにより、タイトな時間内に解き終える道も見えてきます。
何の誘導もない、2次試験の問題に自力で道を開き、真の実力をみにつけていくことがで
きます。
作問者のメッセージをしっかりと受け止められるようになれば、
数学が楽しくなります。
【問題が解けた】というのは、自分の解答と正解が一致しただけの”必要条件”でしかあり
ません。
“作問者の意図が見えた”ときに、初めて心からの満足感が沸き上がるものなのです。
私の個人的見解ですが、
ここ2、3年で解いた記述模試の中でも、ベスト3にはいる良問です。
本日も、最後まで読んでいただき、ありがとうございました。