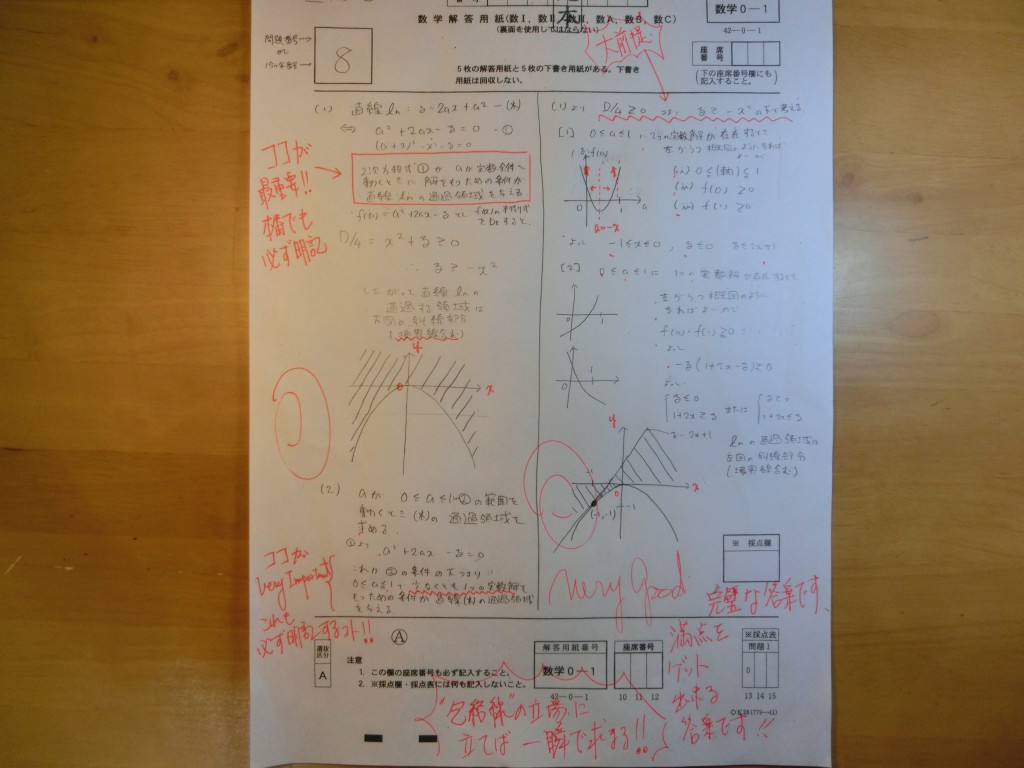
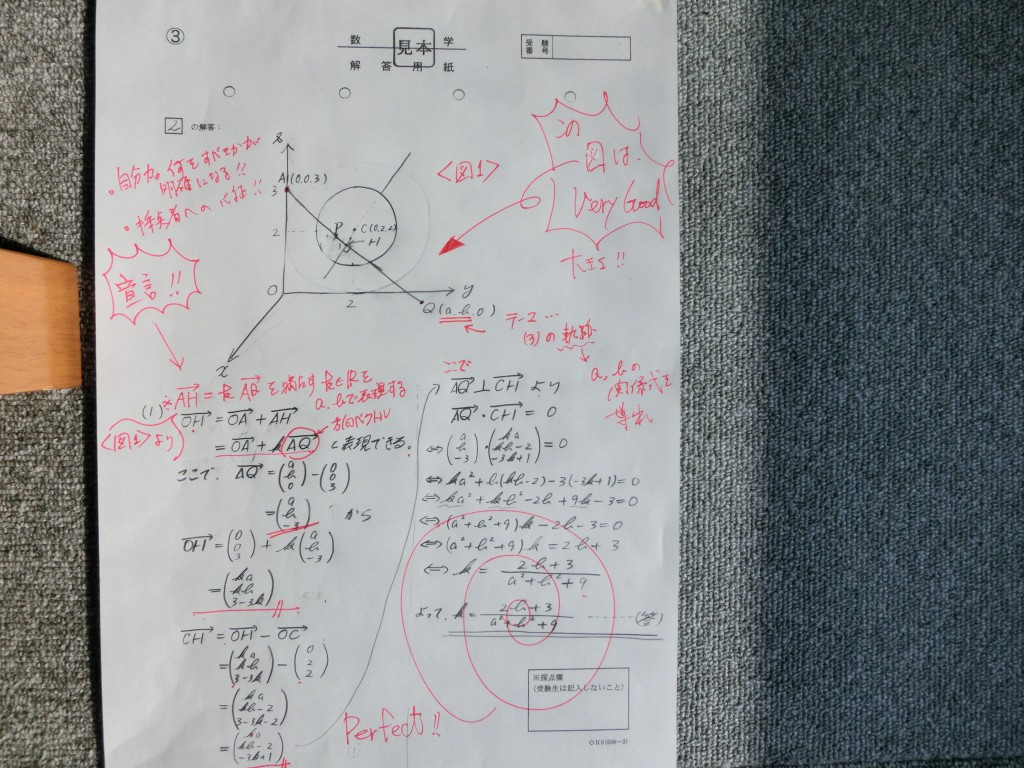
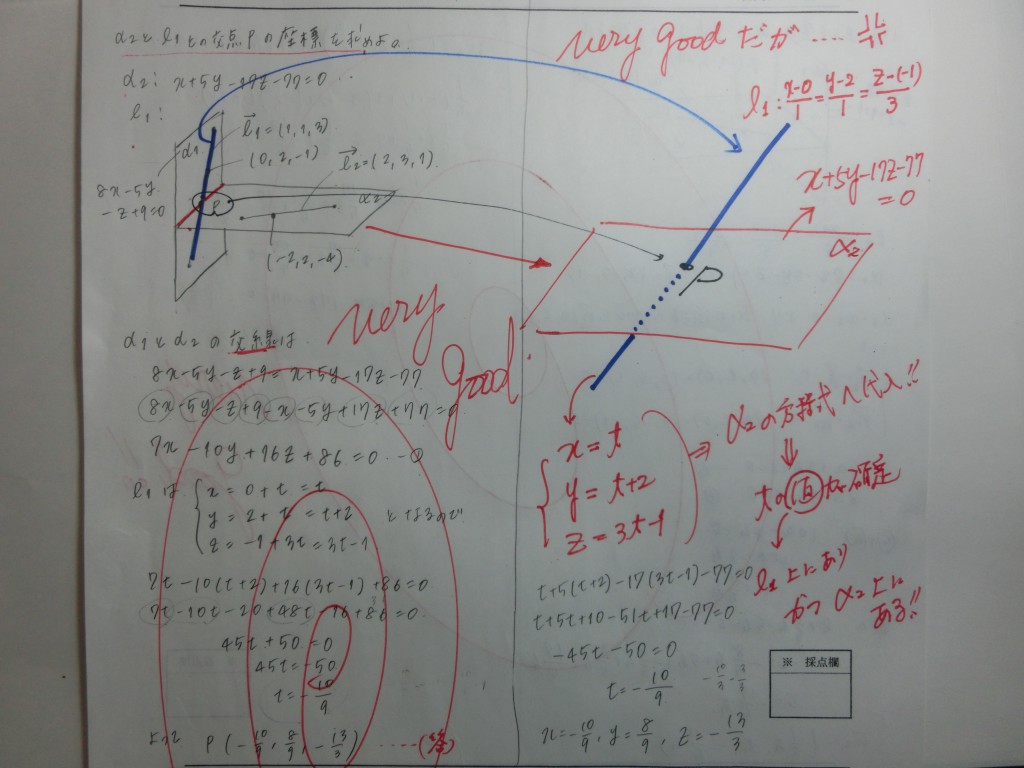
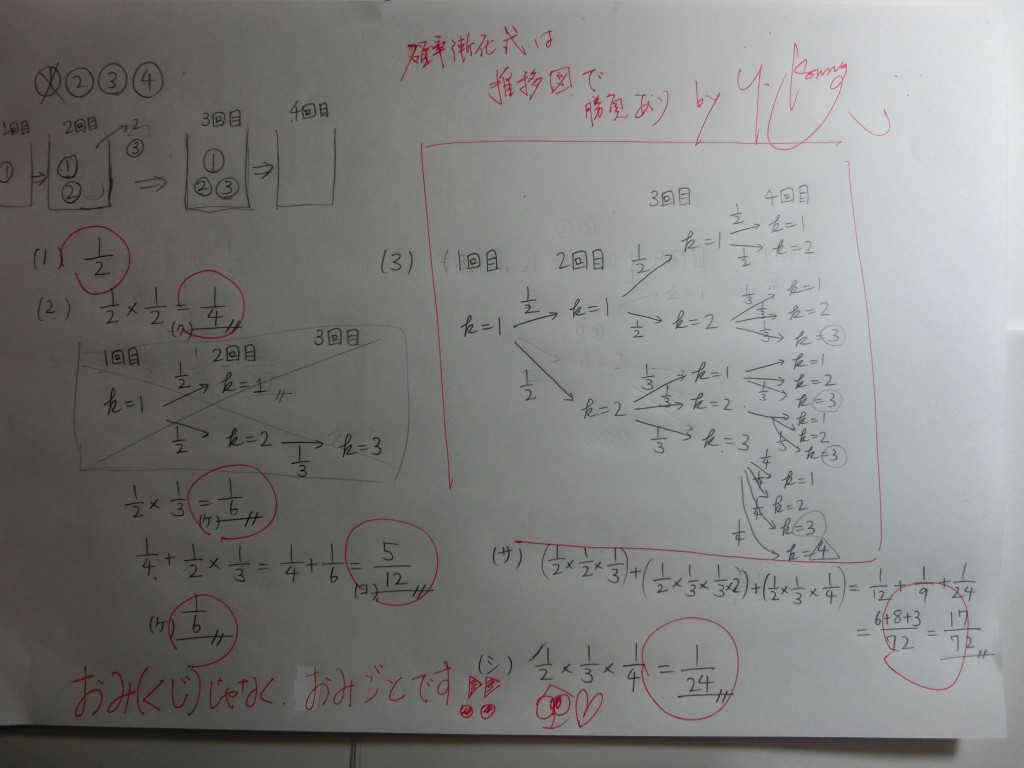
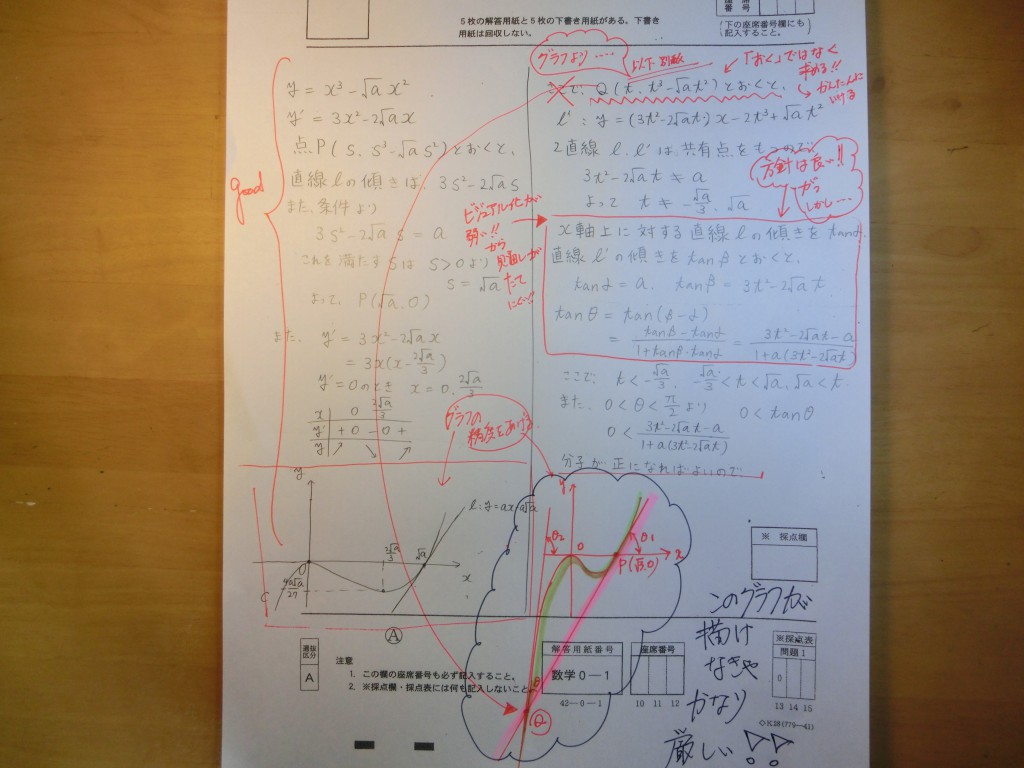
国公立2次記述答案・・・・・・
学校の定期試験、記述模試などの延長で考えてる生徒が大半です。
記述?・・・・・”チャートの説明”みたいな感じで、書けばいい・・・・
このように考えてる生徒も少なくありません・・・・
まず、国公立の2次記述答案と、これらは、全く別物です!!
ここを強く意識するところからスタートです!!
まぁ・・・・『企業秘密』という事もあり、全ては、明かしませんが、裏事情をすこしだ
け教えましょう・・・・
実力養成会には、かつて、某国立大学の入試問題を作成し、採点も担当されていたことの
ある先生もいます!!
記述問題・・・・・
学校の定期試験、記述模試における採点基準は、『どこまで解けたか?』が全てです。
予め、用意された採点基準により一律に採点されます。
当然、点数をつけるための採点です。
一方、大学の2次試験は、『どこまで解けたか?』ではなく、『他の受験生よりどれだけ
すぐれてるか?』なんです!!
すなわち、点数をつけるのではなく、『ふるいにかけるための採点』なんです!!
採点する側は、『ふるいにかける』という基本的スタンスで採点してます。
ここを強烈に意識しなきゃダメ!!・・・・・こういうことなんです!!
ここを意識するのとしないのでは、かき集める部分点の総計は、かなり違ってくるんで
す!!・・・・当然、合否に関わってきます!!
2年前、北大の総合理系に合格した生徒がいます。
この生徒は、2次の手応えとして、数学が一番できなかった・・・・というものでした。
成績開示の結果は、数学が一番成績が良かったんです!!
本人の感覚として、一番悪かった数学が、結果として一番良かった!!
これは、『北大合格者あるある』です・・・よくある話です。
理由は、わかりますね?
『部分点』です!!
実力養成会では、このように、早い時期から、2次記述答案の指導を徹底しておこなって
います!!
今日も、最後まで、読んでいただき、ありがとうございました。