国公立前期試験を明日に控え、
昨日の23日(水)・・・・
実力養成会の受験生たちは、東京、神戸へ
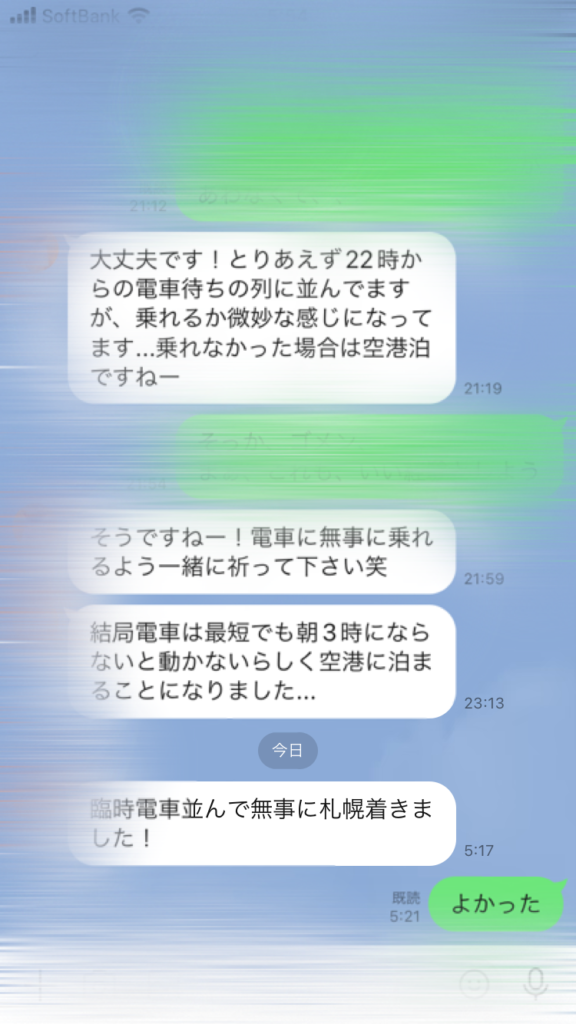
そして、横浜から札幌へ
帯広から札幌へ
それぞれ移動しました・・・・
飛行機は、午前中からかなり遅れてたようです・・・・・・
東京には夕方、到着予定・・・・実際には、22時過ぎに到着・・・という生徒も。
横浜から札幌に移動かけたNさんは・・・・・
これで、本日、私の授業を受けて、旭川へ向かう受験生以外、
全員、移動完了となりました・・・・・・
受験生の皆さんはもちろんのこと、
皆さん以上に、気をもんだ、ご両親の皆さん・・・・
本当に、本当に・・・・・・お疲れ様でした!!
『変わってあげれるなら、自分の命をなげうってでも、変わってあげる!!』
これが、まさに、親の気持ちでしょう・・・・・
ながぁ~い一日がこれでやっと終わってくれました・・・・・・・
本当に、何よりです……
あとは、本人たちの”頑張り”をただ、ただ、信じるだけですね・・・・
いや・・・・信じてあげることしかできません・・・・・・・・・・・
どうか、ご両親の”切なる思い”が本人たちへ届き、
最高のパフォーマンスを決めれるように・・・・・・・・
私も、長女、長男と”親として” 大学受験を経験してます・・・・・・
皆さんのお気持ちは、痛いほどわかります。
本日も、最後まで、読んでいただき、ありがとうございました。