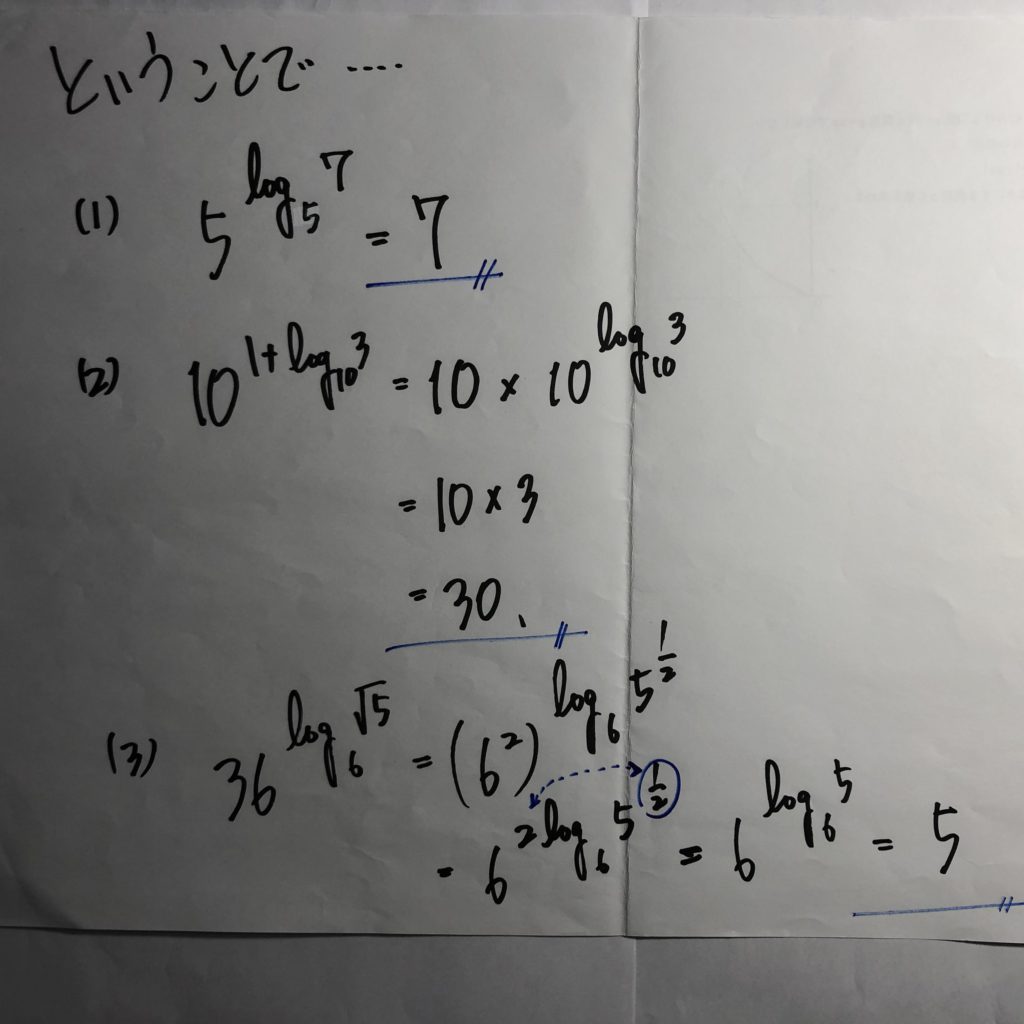札幌北高、高2生、定期対策の指導例をご紹介させていただきます。
今回の定期考査、範囲は “ベクトル全部” です。
札幌北高、全学年に共通しているのが、定期考査では、北大の過去問が頻出!!
週末課題、講習・・・・高2段階で、既に相当数の北大の過去問と向き合ってます!!
この生徒は、既に4step は一通り解き終わってます。
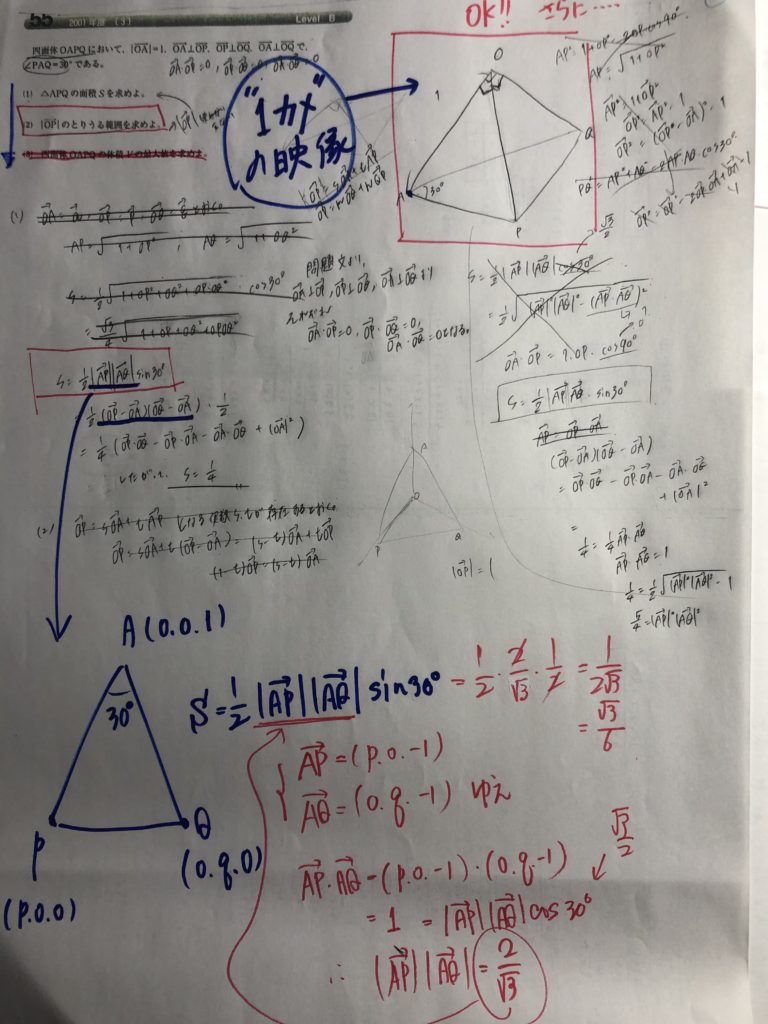
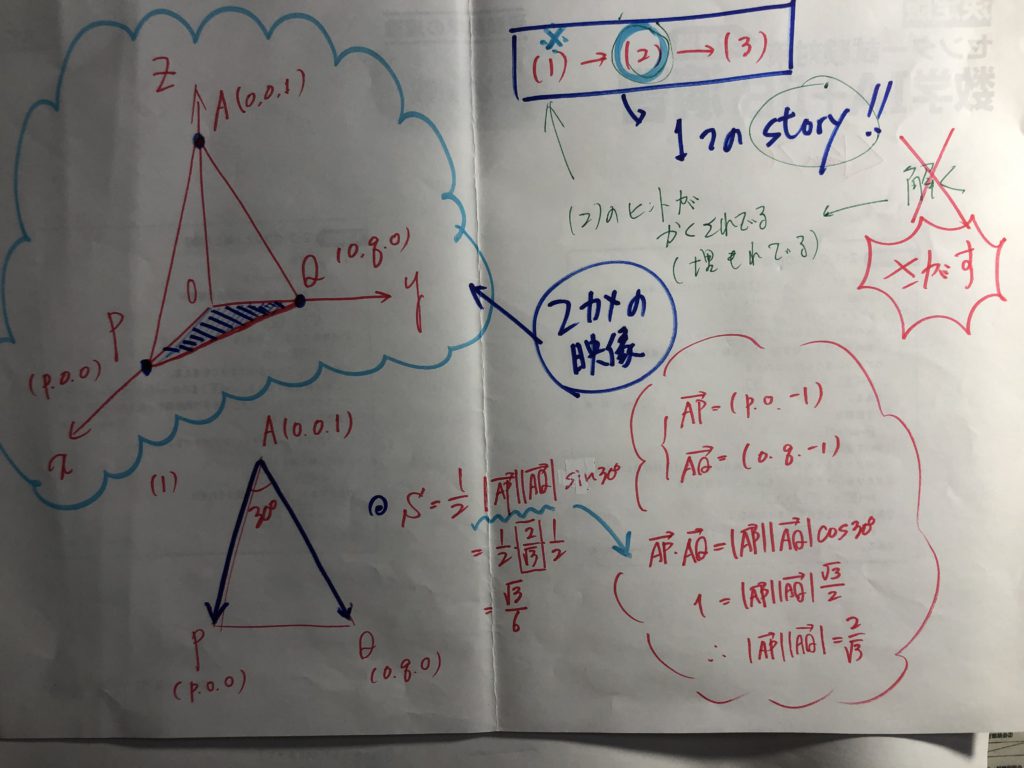
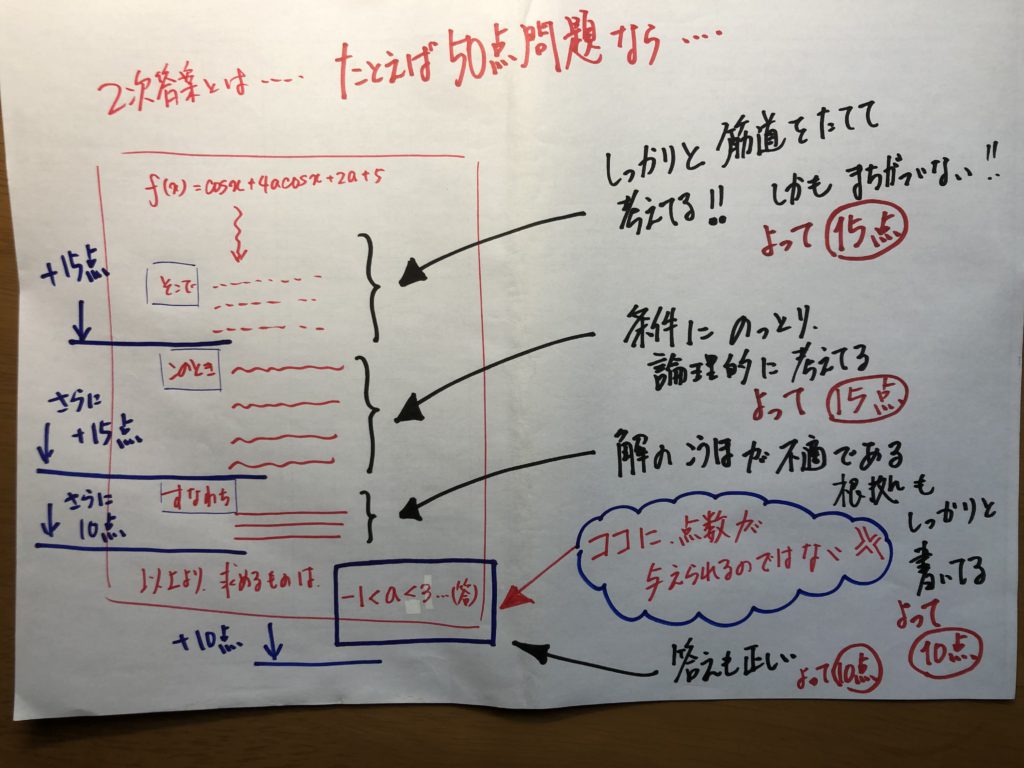
ということで・・・・この問題にチャレンジ!!
『難問』に対して、全然ひるみません!!
この通り!!・・・・・お見事です!! 高2で北大過去問、完答!!
Nさんのお母様!!・・・・・・完璧に解き切ってます!! 素晴らしいです!!
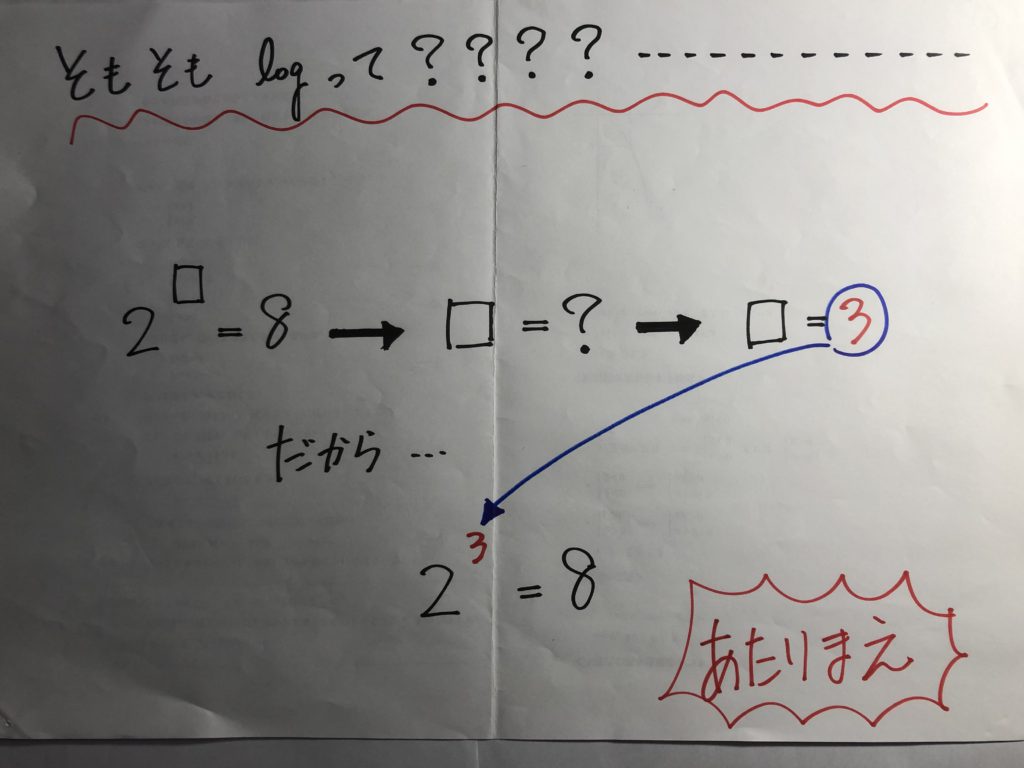
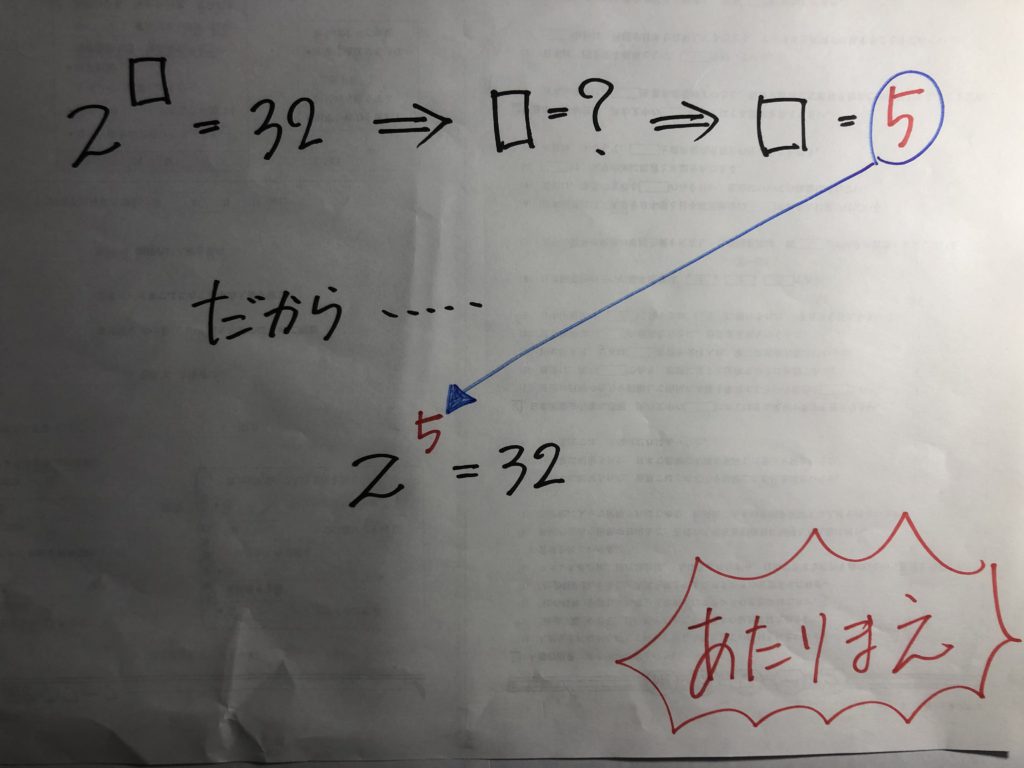
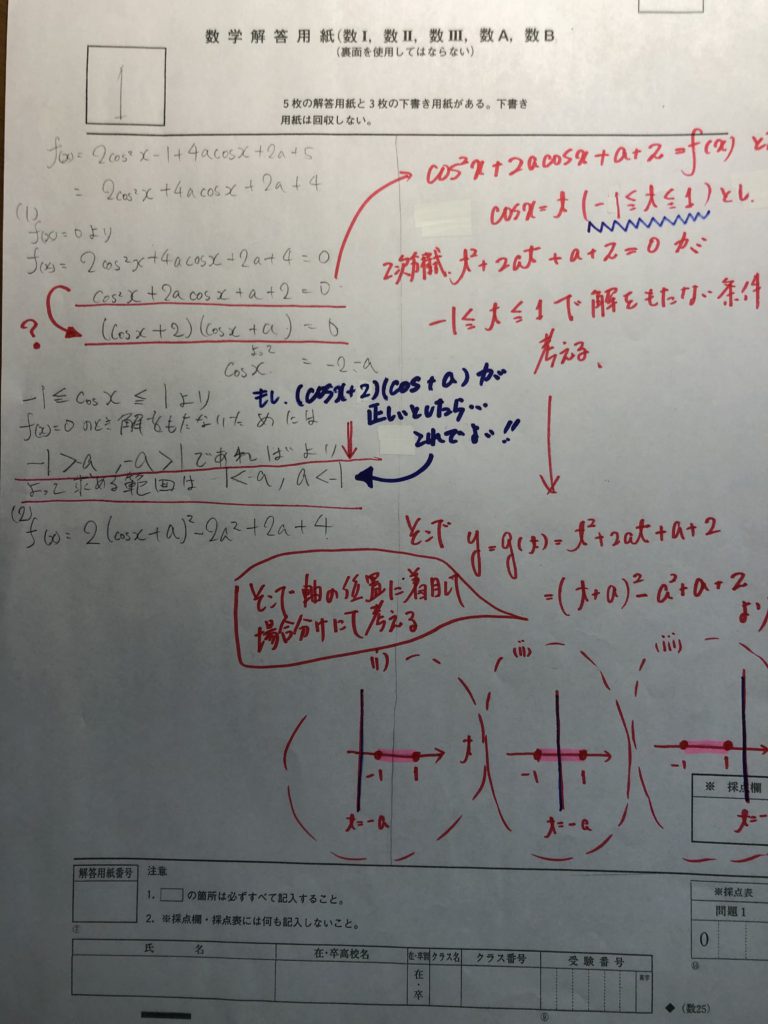
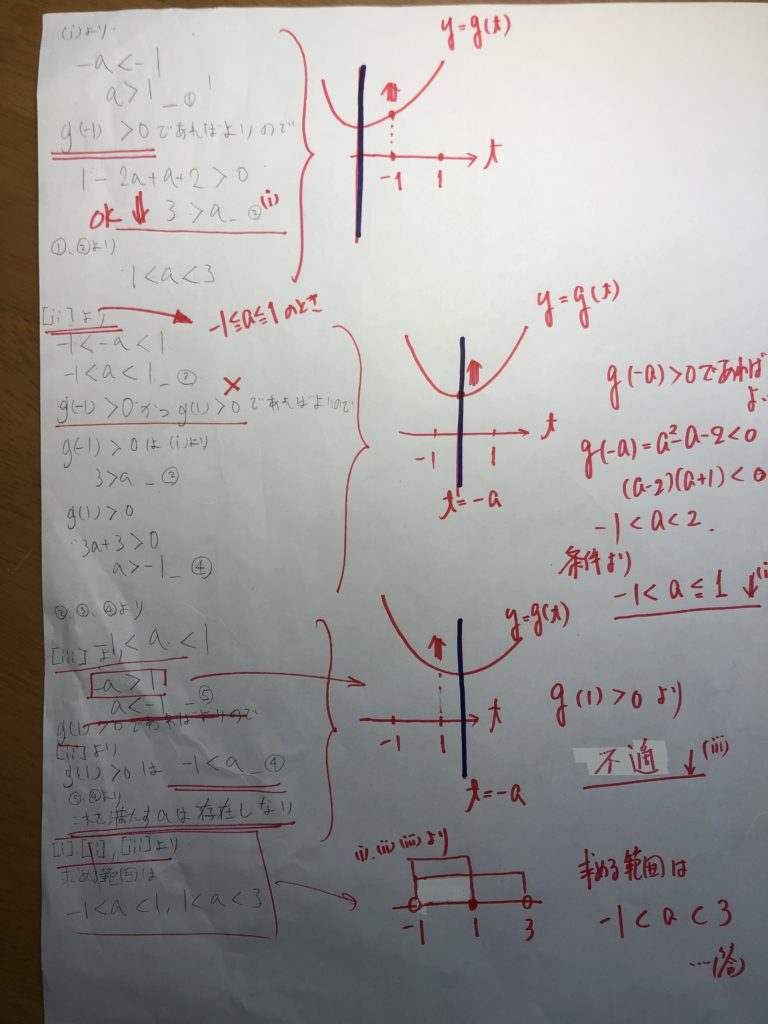
ってことで・・・・思い切って、一橋の過去問にもチャレンジ!!
優秀な北高2年生といえども、やっぱり、一橋の過去問はしんどかったようです。
とはいえ、大健闘!!
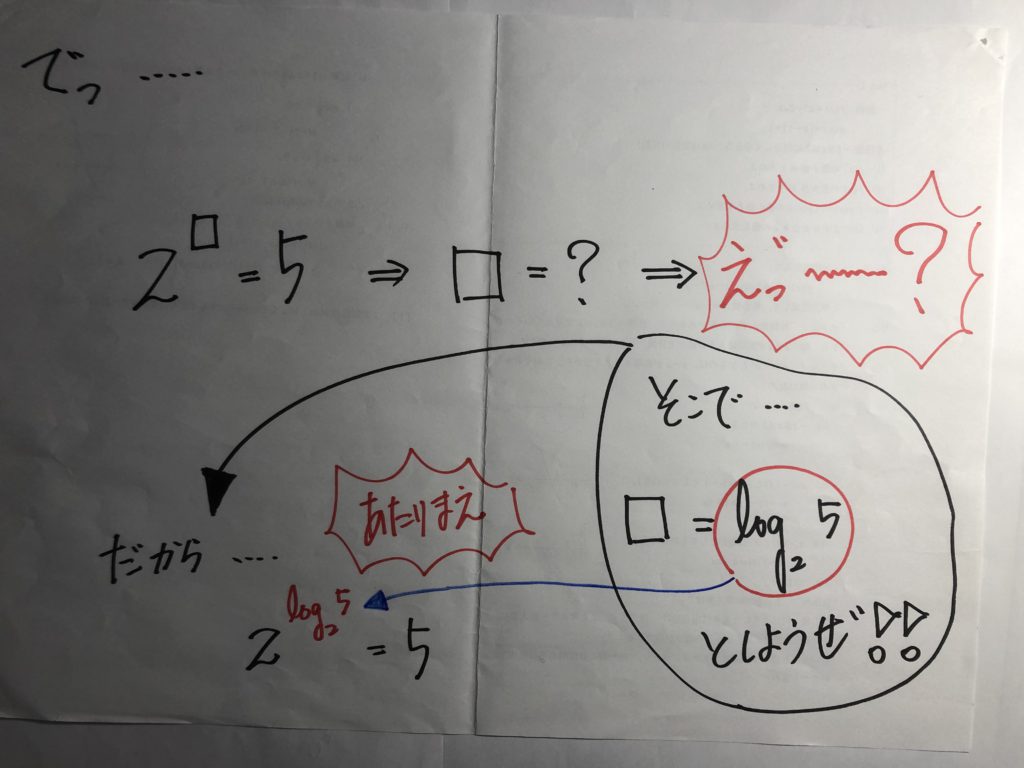
純粋な気持ちで解く ⇒ ヒント、着眼点を本文中から探す!!
こんな気持ちで、問題と向き合うことです!!
このように、その生徒、生徒の定着度に合わせ、対策授業を進めてます!!
他力本願ではない、完全自立を意図しながら指導してます。
本日も、最後まで、読んでいただき、ありがとうございました。