今日は“京大数学対策”の指導例をご紹介させていただきます!!
中学時代は、”普通” の成績でしたが、高校へ進学し徐々に成績を伸ばし、
気付けば、学年トップ、担任の先生から”京大受験”を勧められるレベルにまでになりまし
た・・・・いわゆる”コツコツ型”の典型的な生徒です。
高3生Y君です。
私の持論ですが・・・・
特に京大の場合(阪大も同様)、
『京大の問題が解けるようになる近道は京大の問題をとくしかない!!』
こういう認識でいます。
なぜか?
4年前・・・・実力養成会、初の京大合格者(農学部)を輩出しました。
それまでは、私自身『京大数学』に対して苦手意識をもってました。
しかし・・・・そんなことは言ってられません。
私は・・・・4か月かけて、25年分の京大の過去問をすべて、解き切りました!!
とても、しんどく、大変でした。
しかし・・・・・得たモノはとても大きく、計り知れないものでした。
この経験から、こういう持論になりました。
特に京大数学は、そのほとんどが、誘導がない、独特の切り口となってます。
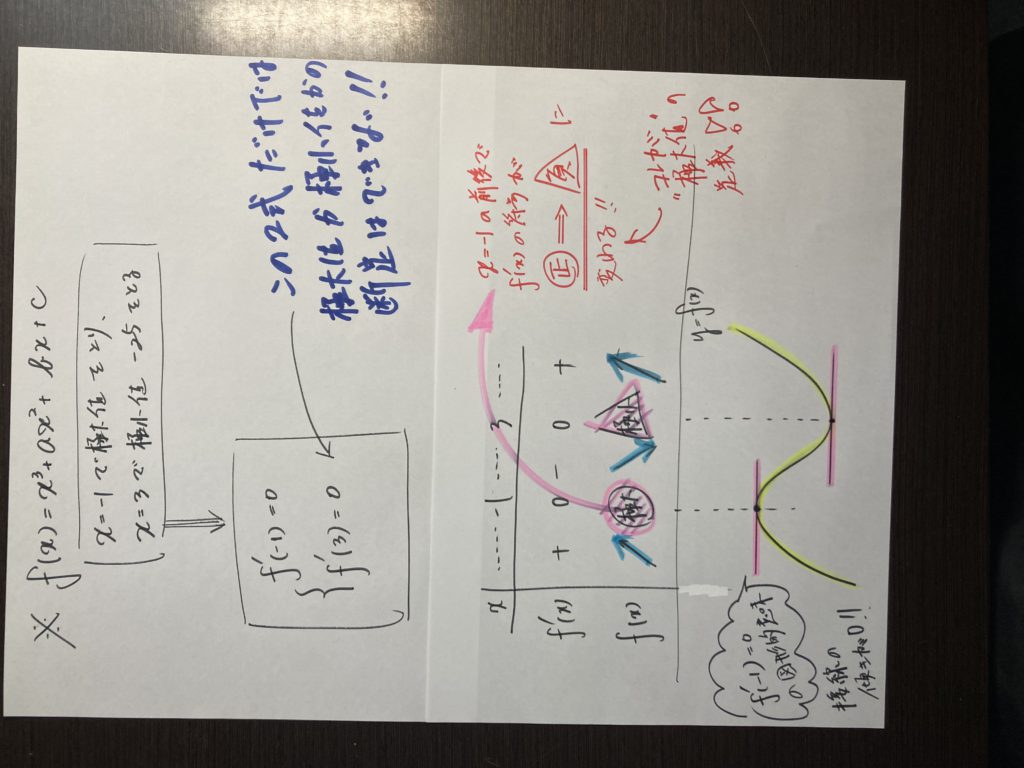
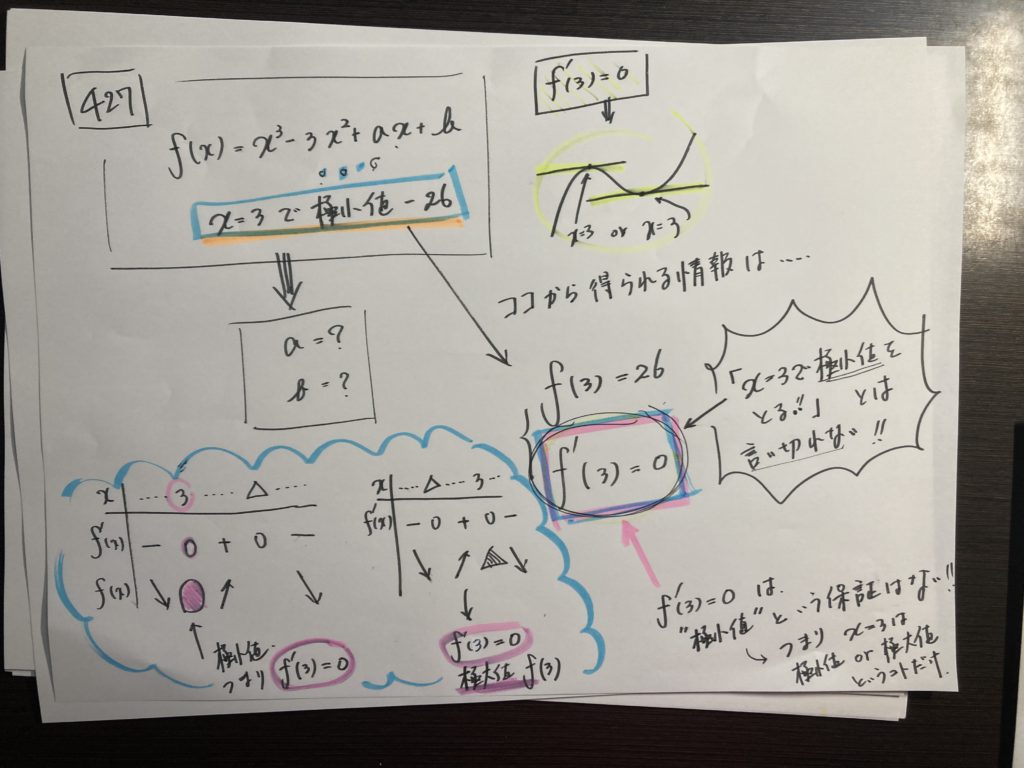
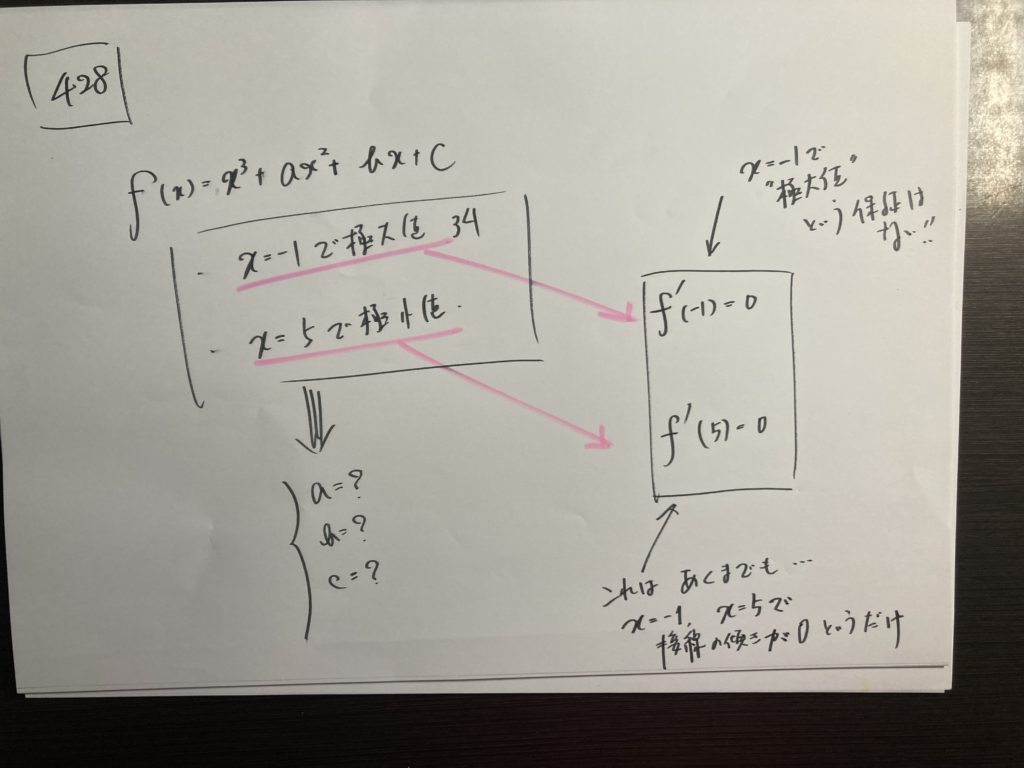
しかも・・・・問題を解くための条件が少ない・・・・
与えられた条件にさらに手を加え、加工しなければ使えない・・・・・
こういう感じの問題がほとんどです。
たとえると・・・・一つの料理を作るうえで、レシピ通りでは作ることが出来なく、
何度も、何度も『下処理』をして取り掛からなければ、料理をすることができない・・・
こんなイメージです!!
これは、25年分、解いたからこそ分かることです!!
以前・・・・どっかの塾ブログで、
『しょせん、東大や数学の問題だって、基礎基本の組み合わせ』
というのを見たことがあります・・・・・
こう言うことを書くヒトは、実際に京大数学を解いたことのないヒトです。
東大にしても京大にしても”世界的な数学の学者さん”の作る問題です。
まず・・・・そういった問題に対して・・・・“リスペクト”の気持ちで
真摯に向き合う・・・・・
そうすると・・・・・こんなコメントになるはずはありません(笑)
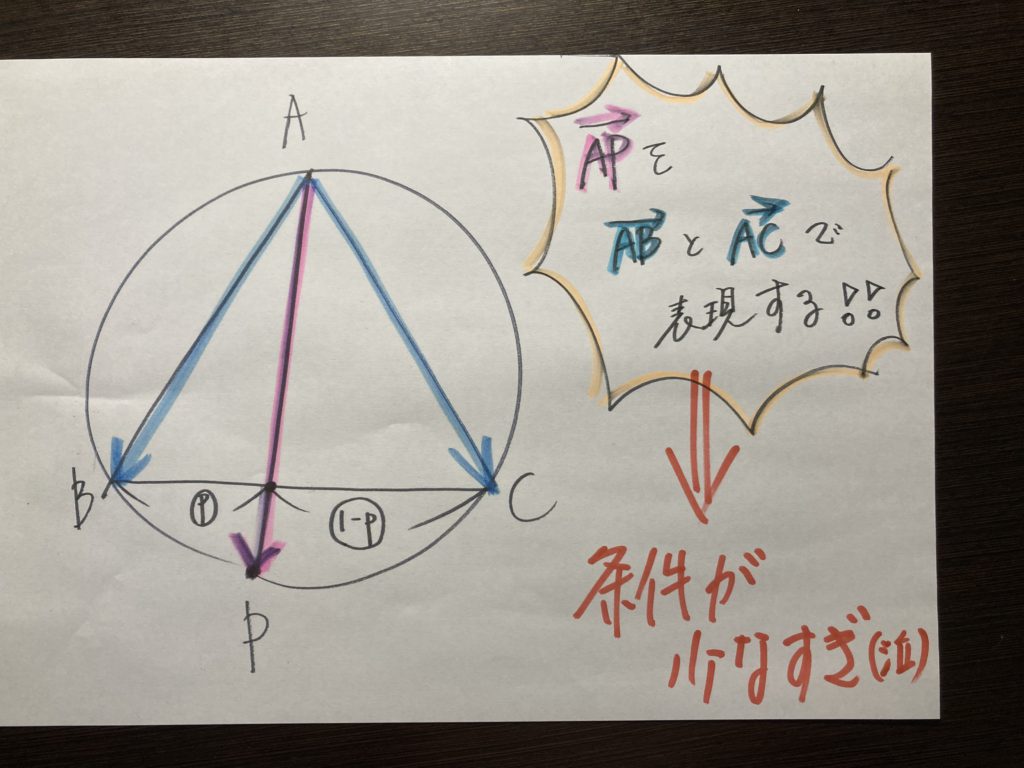
さて・・・・この日は、この問題を取り上げました・・・・
図示すると・・・・
条件、少なすぎ(泣)
これが・・・・・京大の独特な”切り口” です・・・・
例えば・・・・これが北大だとすると・・・・
問1、問2 と誘導がついて・・・・・
最後に問3でAPベクトルを求めさせる・・・・という出題になります。
つまり・・・
問3を解くために、問1、問2の結果をどう橋渡しするか?
こういう着眼点をもって・・・問題を”斜め方から”ずる賢く見ていく!!
こういう向き合い方です。
しかし・・・・京大は、唐突に”APベクトルを求めよ” なんです・・・・・
この続きは・・・・明日の実力養成会通信に書かせていただきます。
本日も、最後まで、読んでいただき、ありがとうございました。