-
Category / カテゴリー
-
Recent Articles / 最近の記事5件
- 2026/1/30
2026年、新年度新規受付、定員となりました!! - 2026/1/30
実力養成会通信 第3134号 ”札幌南高で数学学年1位達成!!” の巻 - 2026/1/29
『極王餃子の王将ラーメン』 - 2026/1/29
実力養成会通信 第3133号 ”昨日の保護者通信” の巻 - 2026/1/28
『やりたいことを探しに行く!!』でいいのです。
- 2026/1/30
-
Archive / アーカイブ
ニュース・ブログ
今朝も5:45から早朝スカイプ授業です。
見たいワールドカップを見ずに、早朝ランニングをしてきました!!
ブログも授業前に更新させてもらってます。
今朝は、早朝授業だから・・・・
だとか
仕事が立て込んでるから・・・・更新できません(泣)
そんなことはしません。
私自身も・・・・”継続こそ力なり” の精神で行動してます。
さて・・AO入試、指定校推薦等で、合格が内々定してる生徒が数名おります。
そこで、”入れ替え” という形で この度、数名の新入会がありました。
その中の一人・・・・・
道北のとある町の中1生です。
札幌南高を志望してます!!
この生徒は、いわゆる ”僻地校” に通ってます。
私も、臨時教員時代、”僻地校” でも働かせてもらいました。
“僻地校” には、”僻地校” ならでらのいいところ、そうでないところ、色々あります。
特に”勉強”に関しては、地域の実情もありとても”悩ましい”現実があります。
縁あってこの度、入会となりました!!
道北の人口4000人にも満たない小さな町の僻地校から、
札幌南高校へ進学、そして、国立医学部現役合格!!
かならず、実現させましょう!!
ハッキリ言いましょう!!
札幌南高校合格は、単なる通過点でしかありません!!
1対1のスカイプ授業だから実現できます!!
ちなみに・・・・スカイプ授業で帯広柏葉高校に合格し、
3年間オールスカイプ授業で北大総合理系に現役合格した生徒もいます!!
現在、実力養成会で非常勤講師としてバイトしてもらってます!!
F先生です!!
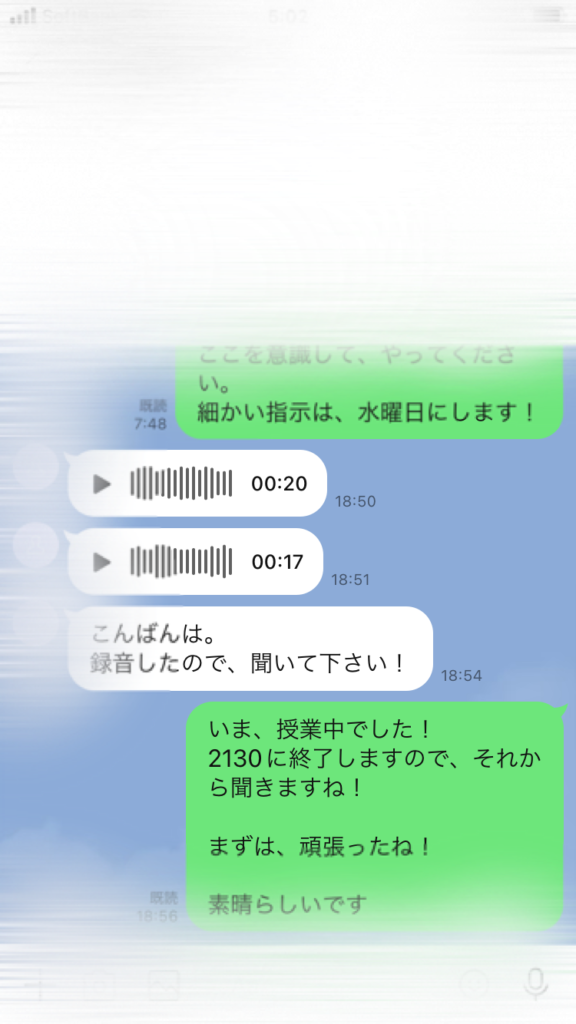
さて、そんな生徒から昨晩早速“音読”の報告もありました!!
継続こそ力なり!!
凡事徹底!!
僻地校であろうが、なかろうが、この2つさえ、実行することで、
必ず実現可能!! このことを実証していきましょう!!
思い立った今がスタートです!!
本日も、最後まで、読んでいただき、ありがとうございました。
トップ高の生徒でも、いまだに、こんな初歩的なミスをします!!
日本語に引っ張られ過ぎ!!
ちなみに・・・
It is kind of him to give me the information in advance.
『ヒトの性質・性格』を表す形容詞のときは『of』・・・と勉強しましたね?
“こういうものなんだ” と機械的に教えられたことでしょう・・・
では・・・・なぜ『of』なのでしょうか?
明確な理由というか、当たり前の理由があります。
そもそも・・・・『of』の原義は、 “全体から、そのを一部を取り出す”
a piece of cake なら『ケーキ全体から、その一部を取り出す』というコト。
a student of school なら『その学校全体から、一人の生徒を取り出す』というコト。
だから、
『性格(性質) of 人』というのは、その人から、その人を構成する性格(性質)の一部が
出てきたね!!・・・・・というコトです。
これって・・・・当たり前!!
ネイティブはこんな感覚です!!
何でもかんでも・・・・機械的に覚えてきた、というより機械的に教えこまれてきたから
日本語に引っ張られる!! ということです。
本日も、最後まで、読んでいただき、ありがとうございました。
ある生徒が、ある大学の獣医学部の指定校推薦を受け、
校内選考をクリアーし、今週末に面接・小論文を受けます。
獣医学部・・・・
ずぐ、動物病院の先生? とイメージしがちですが、実に多岐にわたります!!
獣医師はペットや家畜だけでなく野生動物の診療もします。
あるいは、都道府県の食肉衛生検査所で家畜の生体検査も!!
もちろん、民間企業での研究職だって・・・・・
さて・・・・獣医をされているあるお父様から、
獣医学部の指定校推薦の本試験に臨む、ある生徒へ
お忙しい中、貴重なラインをいただきました!!
また、実力養成会の現高1生の中にも、獣医学部を志望してる生徒もいます!!
獣医学部のリアルな内情を垣間見ることのできる、
大変に貴重で説得力ある内容です。
この場で、ご紹介させていただきます!!
ブログへの掲載については、事前にお父様のご了承をいただいてます!!
『入学前から方向性を決めない方が良い』
『6年間、入学前のテンションを維持し勉強』
とても重たく、そして説得力のあるお言葉です。
お父様・・・・改めまして、お忙しい中、ありがとうございました。
本日も、最後まで、読んでいただき、ありがとうございました。
医師をされてるお父様のご意見・アドバイスにしっかりと耳を傾けてます!!
私自身が、これまでのコロナの教訓を生かして、今できることをしっかりと行う!!
手洗い、うがいはもちろんのコト、
率先して、外出自粛!!・・・・・・・ステイホームに徹してます!!
第8波・・・・”1月のピーク” 1日のコロナ感染者は3万人近くになると予想されてます。
その時になって、緊急事態宣言を発令して、どうだ、こうだと言っても、
時すでに遅し!!
だそうです。
当然ながら・・・・受験にも影響は出るでしょうし、一部に変更も生じることでしょう。
今から、やれることはやる!!
私の”おうち時間”は・・・・・ジグゾーパズル!!
今年の1月に、少しだけ手を付け、そのまま放置してあった”赤富士”です・・・・
◆着手1日目
◆着手2日目
◆着手3日目
◆昨日の状況です!! ここまで進みました。明日完成予定です。
本日も、最後まで、読んでいただき、ありがとうございました。