-
Category / カテゴリー
-
Recent Articles / 最近の記事5件
- 2026/3/13
◆cafe ノスタルジア 三石町 - 2026/3/13
実力養成会通信 第3177号 ”本気で北大を目指してるキミへ” の巻 - 2026/3/12
3.11から一夜明けて・・・ - 2026/3/12
実力養成会通信 第3176号 ”浪人? 進路選択について” の巻 - 2026/3/11
★★豚丼/とんすけ 千歳市東郊
- 2026/3/13
-
Archive / アーカイブ
ニュース・ブログ
『今さ、先生の示したやり方で、やってごらん!!』
生徒へこう伝えます。
生徒は、見よう見まねで、やります。
正解にたどり着きます。
要は、生徒にやらせる。
自分の手で解かせるって事です。
見よう見まね・・・・・これでいいんです。
中には、一から十まで、手とり足とり説明して、理解させようとする講師もいるでしょ
う・・・・・・これが『理解させられる』・・・・・
(強制的に)『理解させる』⇒『演習させる』
すなわち、『理解させる』ことを第一に考える講師の人たちって多いように思います。
これも、これで”あり”だとは思うですが・・・・・
やはり、『理解』の前に、『できる』があれば、より理解しやすくなるんです。
『理解』ってことは、心理的な苦手意識の問題では?
『できる』・・・・・・このあとに、理屈とか、成り立ちを説明します。
生徒は、例外なく、『なるほど!!』ってなります。
そこから、本質論に入っていきます・・・・・・・
指導の”スタイル”とか、”組み立て”は、その生徒の状況、到達度を考え、臨機応変に使
い分けてます。
今日も、最後まで、読んでいただき、ありがとうございました。
ある大学としておきます。
そして、ある大学教員(私の友人)としておきます。
その大学は、毎年、新入生向けにオリエンテーション合宿を実施しています。
新入生のクラス単位で実施され、上級生が主催・企画するイベントです。
このオリエンテーション合宿の参加は義務ではなく任意だそうです。
ある大学教員がこうぼやいてました・・・・・
年々、このオリエンテーション合宿に参加する新入生が減っている。
ここ最近の学生の特徴は、単に勉強できるだけ。
だから、大学になじめない学生が激増している。
“友人を作ることに何のメリットがあるんですか?”
と真顔で反論する学生もいる。
参加しなかった学生に、何故?って聞くと”親が参加しなくてもいい”と言った、と。
優秀なんだけど、言われたことしかやらないし、
自分で壁を作って引きこもってしまう。
自主性のかけらもない、
あれじゃ、就職なんてとても無理だわ・・・・・・・
こんなことをぼやいてました。
私も、この話を聞いた時、素直に納得しました。
事実、私も、このような受験生の指導を担当させてもらったこともあります。
挨拶ができない・・・・・・・・・・・
周囲とうまくなじめない・・・・・・・
自主的に動けない・・・・・・・・・・
“出来ない事”の言い訳を常に考えてる・・
悲しいことに、コミュニケーション能力が足りない、というより、完全に欠落してるんです。
どうして、このような学生が激増してるんでしょう?
ズバリ、幼少期からの慢性的な親の過干渉です。
よく、『こんなことも、出来ないの!!』と感情的になって叱るお母様がいます。
『こんなことも出来ない』のは、『こんなことも』やらせてないからです。
先日、たまたま、偶然にも、尾木ママの子育てに関するテレビ番組をみました。
その中で・・・・・・
近ごろでは、
朝は、『早く、起きなさい』から始まって、
夜は、『早く、寝なさい』まで、子供の顔を見れば叱ってばかりいるお母さんも珍しく
ない。そんな母親に限って、『うちの子は何もできない』と愚痴をこぼすそうです。
母親が叱って子供に行動を促すことが、子供の自立心を発達させる大きな障害になって
る。・・・・・このようにコメントされてました。
私も、全くの同感です。
今日も、最後まで、読んでいただきありがとうございました。
滝のようにしたたり落ちる汗。
もう限界?
いや、いや・・・・・あと一分。
サウナの中にセットされた時計の秒針の進みがやけに遅く感じる。
一分経った!!
足早にサウナを出る!!
かけ湯で、サーっと汗を流し、
一気に水風呂につかる・・・・・・
まさに、至福のひととき。
体中から体温がさ~っと引いていく感覚。
体中のアルコールが水風呂に吸い込まれていく感覚。
合わせて、体中に蓄積された疲労も一緒になって・・・・・
これらの感覚が、水風呂の醍醐味だろう。
確かに、水風呂につかった翌日は、体調もすこぶる良い。
アタマの”キレ”もすこぶる良い。
つい、1年前までは、水風呂に入れなかった自分・・・・・
今となっては、水風呂はなくてはならない。
水風呂に入るたびに、
『もうダメってまで我慢して、そのあとは、一気に(水風呂に)入るだけ』
とアドバイスしてくれた友人を思い出す・・・・・
“水風呂”と出会えたのも、この友人のおかげだ。
今日も、最後まで、読んでいただき、ありがとうございました。
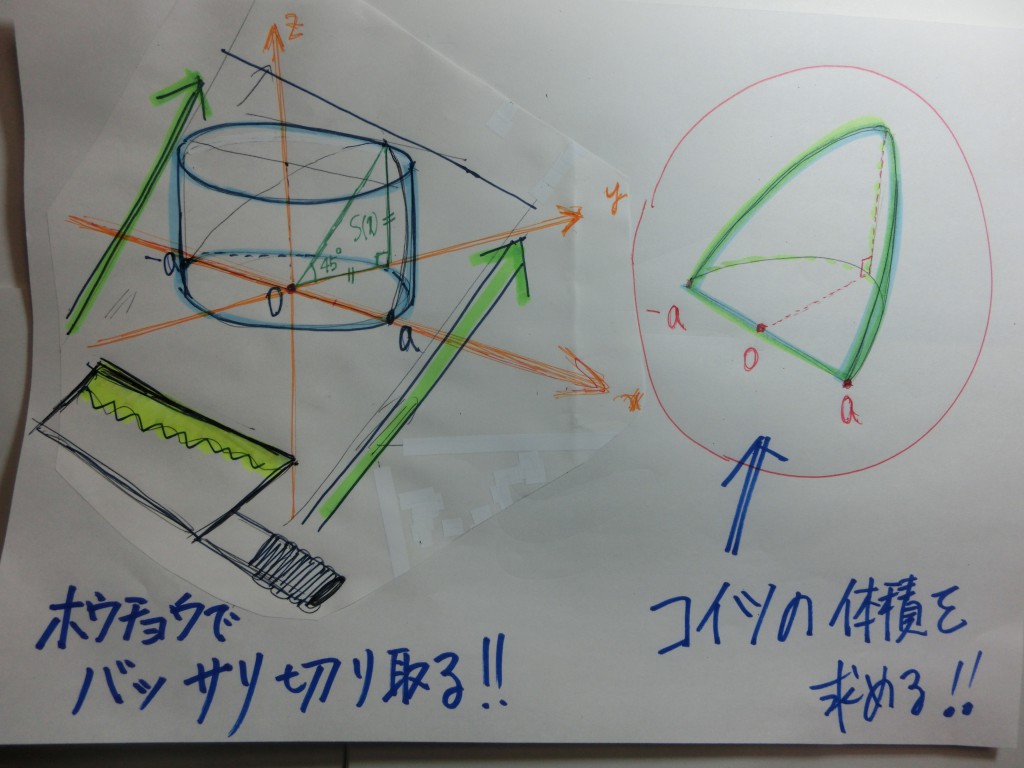
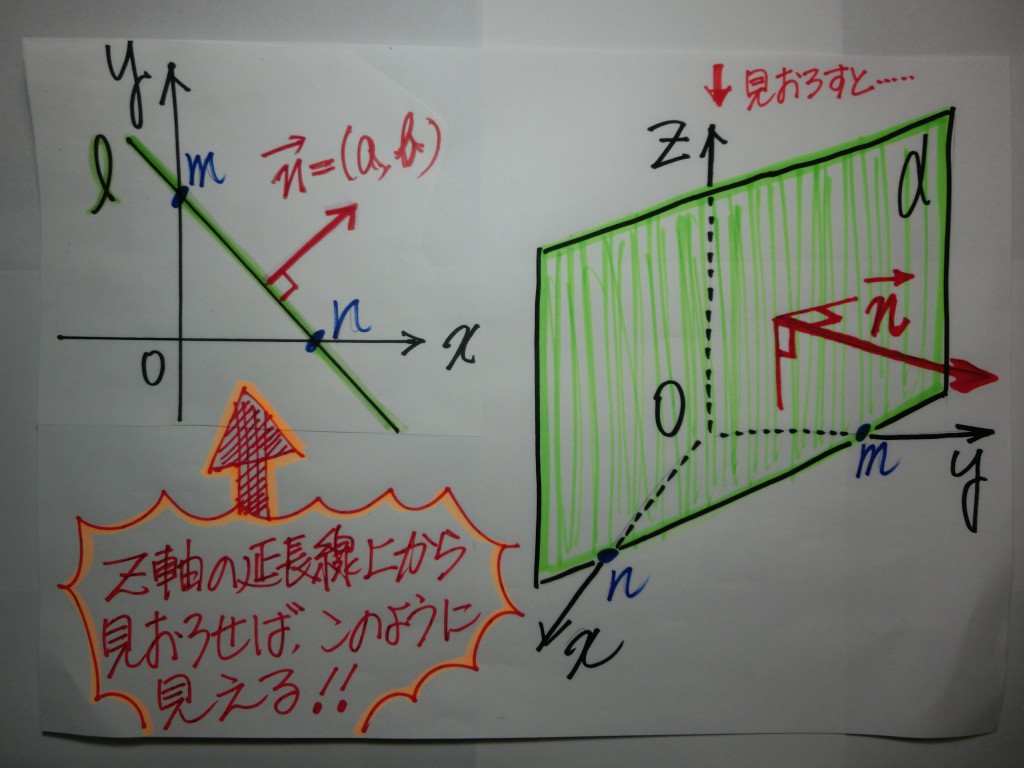
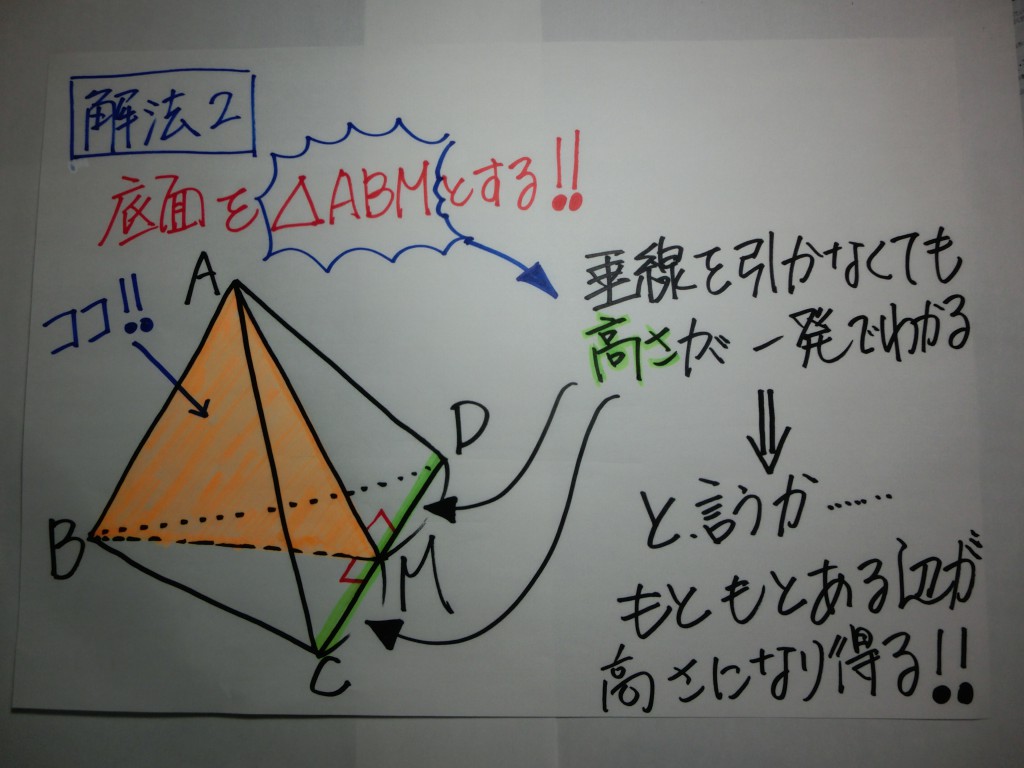
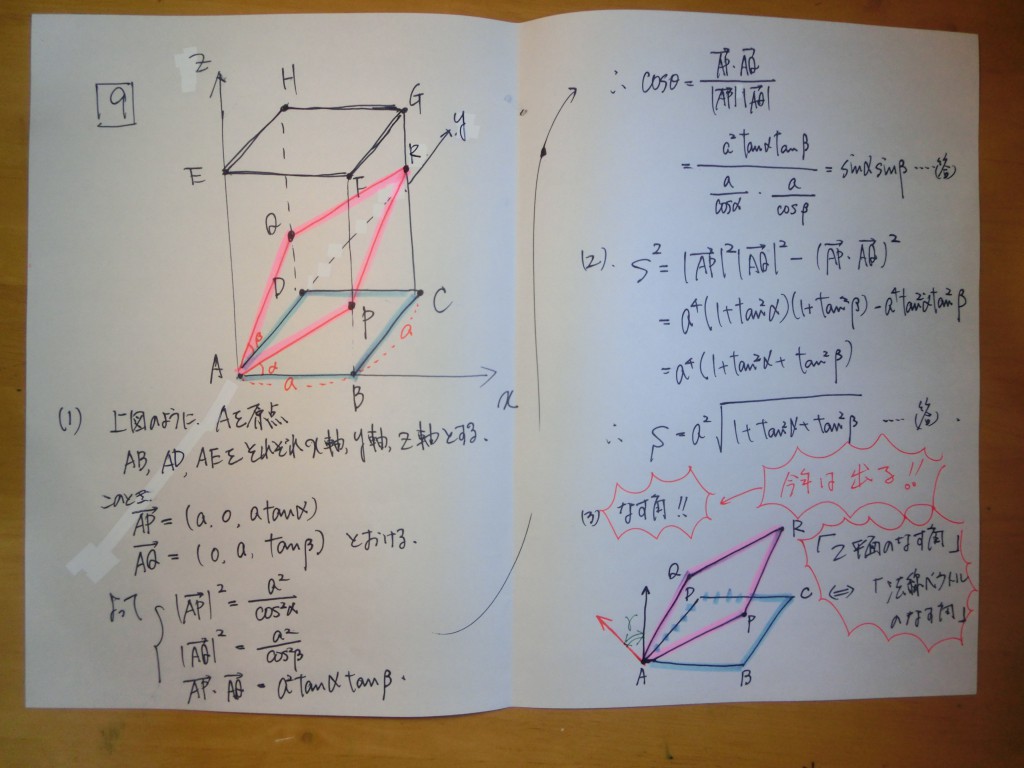
『運動神経が良い』 ⇒ 自分のイメージした通りに体を動かすことが出来る。
『空間図形に強い』⇒ 問題文から自分のイメージした通りに空間図形を把握できる。
なんだか、とても似てる感じがするのです。
なにか、相通ずるものがあるような気がするんです。
これを、『図形的センス』と呼ぶ人もいます。
しかし、私は、『センス』って言葉は、好きではないし、使いません。
あえて、言うなら、『壁』。
別に、空間図形に精通するには、運動神経が必要ってことではありません。
そもそも、数学は、『考えることそのもの』を扱う教科です。
そこに、出てくる数字だとか、公式、定理なんてものは、道具にしかすぎません。
数学の骨格をなすものは、『徹底した論理』です。
自分の頭をどれだけ働かせることができるか? が問われます。
論理的に考えるってどういうことか?
わからないって、どういうことか? を知り、
それを突破するには、どうすればいいか?
そういう時に、『壁』が立ちはだかります……
もちろん、これらの『壁』を克服するためのトレーニング法は、いくらでもあります。
『センス』の問題として、簡単に片づけるべき問題じゃありません。
今日も、最後まで、読んでいただき、ありがとうございました。