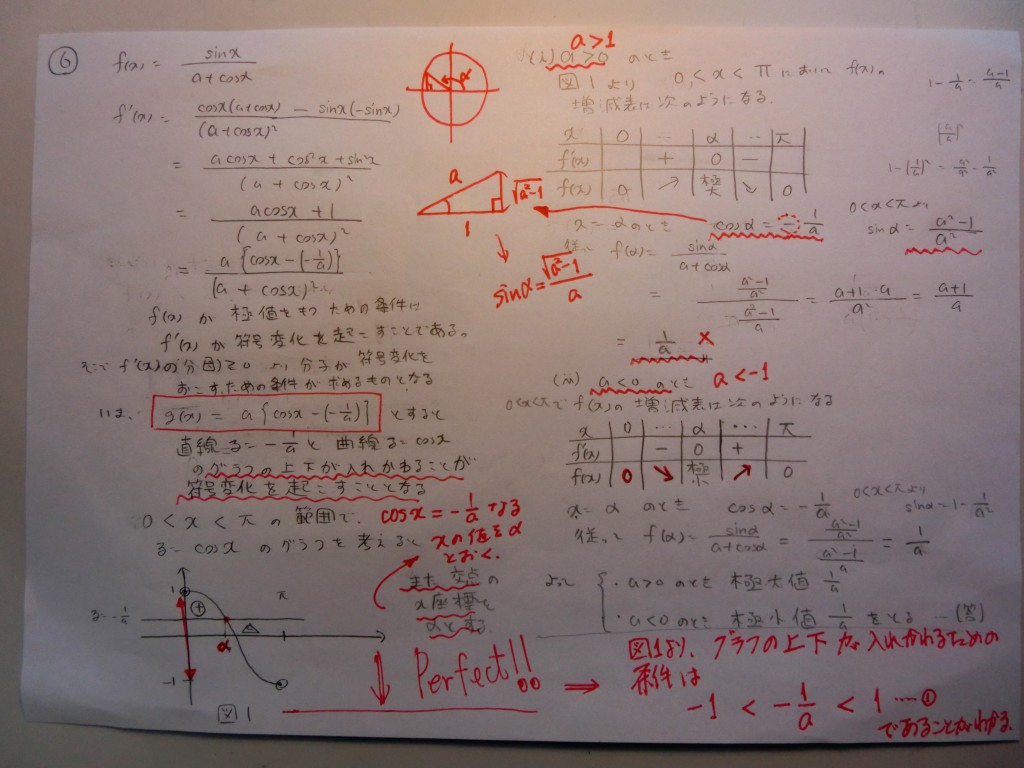
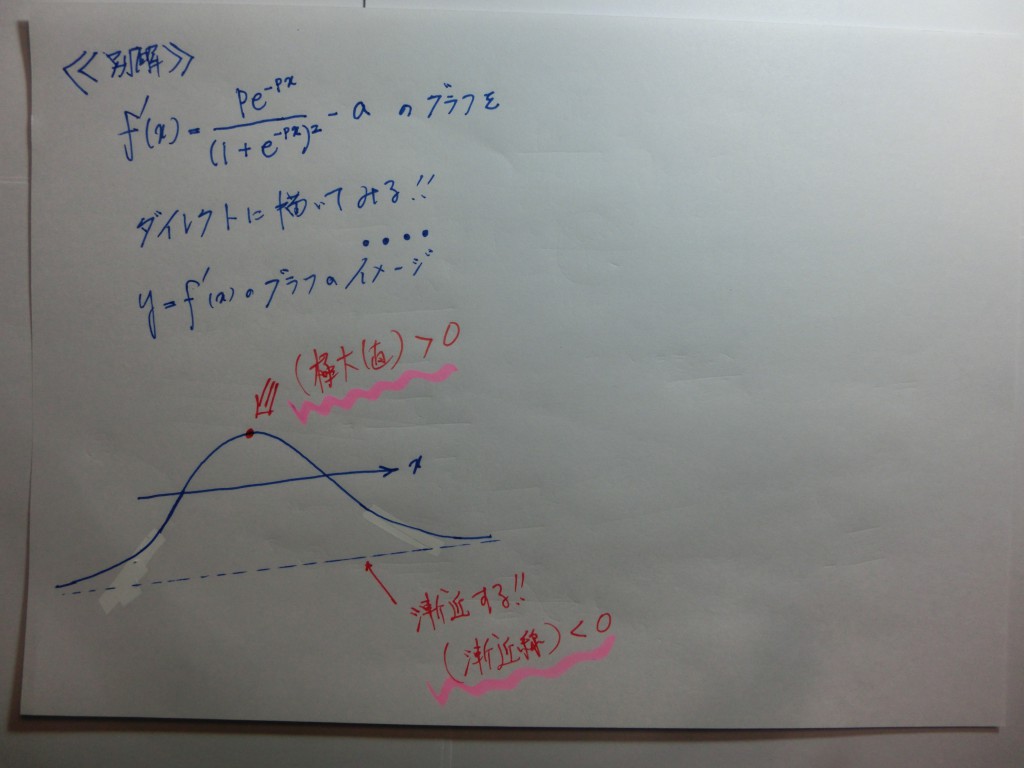
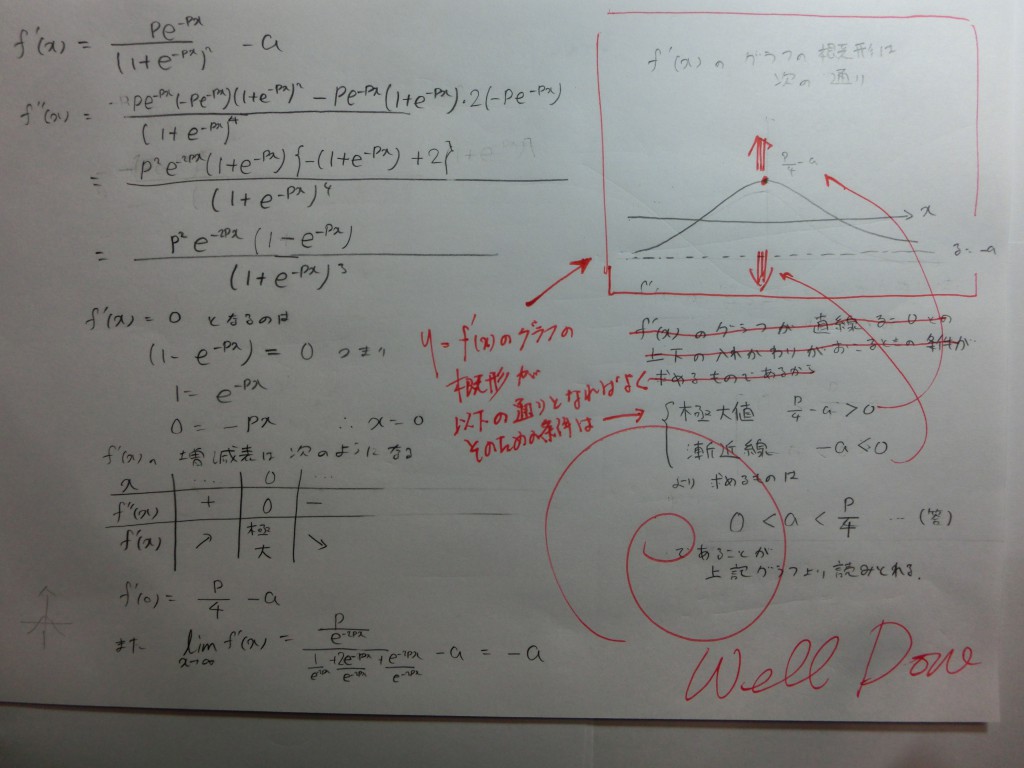
★度々、このブログに登場してもらっている、この本・・・・・
今日、ご紹介させていただきたい内容は・・・・・・・
『本は内容だけじゃなく、気持ちを贈るもの』

またまた、ある一節を抜粋させていただきます・・・・・・
———————————————————————————————————-
冒頭にも書きましたが、私は本をほとんど読みません。
そんな私が野口嘉則氏の『鏡の法則』(総合法令)という本を手にしました。
「読んだ人の9割が涙した感動のストーリー」ということで数年前にベストセラーに
なった一冊だそうです。
(中略)
読んでみると私も涙があふれてしまいました。
自分の周りに起こっていることのすべては、自分に原因がある。
ということに共感し、涙した私は、いろいろな方々にこの本をプレゼントさせていただ
きました。
ただし、私がプレゼントしたのは、本だけではありません。
お贈りさせていただいた人への私の思いと『私は、この本を読んでこんなことを感じま
した』という自分の感性を一緒にお贈りしているつもりなのです。
(中略)
本というものは、ただ読むだけでなく、人に贈ったりすることで自分という人間を相手
に理解してもらえたり、相手をより深く理解したりするものなのかもしれません。
———————————————————————————————————-
私自身、職業がら、本をプレゼントしていただくことがあります。
大切に、じっくりと読ませてもらってます。
もちろん、贈ってくださった方の感性を感じながら・・・・・・・
今日も、最後まで、読んでいただき、ありがとうございました。