『自称プロの家庭教師』のブログです・・・・・・
誰? とか どこの? はもちろんどうでもいい話。
要は、保護者のみなさんに”シビアな目”を持っていただきたい!!
そのために、あえて、紹介させてもらいます。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
目標にしている大学は、いわゆる難関国立大学ですから、現役合格
を目指すならば、これくらいの時期から、順調に伸び続けていくこ
とが大切です。
その辺りに気を配り、しっかりとした演習を実施し、高みを目指し
て指導します。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
このように、口先だけの、実行のともなわない、適当なコメントに対して、メチャクチャ腹が立ってしまいます。同業者として、絶対に許せません。
まず・・・『現役合格を目指すならば』の部分に関して・・・・・
自称プロの家庭教師ならば、現役合格のみを考えて指導しなきゃダメでしょう!!
指導する側は、(成績が)ギリギリでも、なりふり構わず、最後のひとつの椅子に滑り込ま
せる!!そんな気持ちでなきゃだめ。これじゃ”傍観者”・・この時点で、話になりません。
次に・・・『順調に伸び続けることが大切です』の部分に関して・・・・
順調に”伸びつづけたい”たいから、家庭教師をつけたのでは?
『しっかりとした演習』『高みを目指して指導』の部分について・・・・
なんら、具体性がない。具体的にどうやっていくのでしょうか?
高みって具体的に、どういうことでしょうか?
出まかせで言ってるだけ。
私は、『批判』だけでは終りません。
ということで、・・・・・・・・
じゃ、どう取り組ませるのか?
『しっかりとした演習』ってどういうことか?
実力養成会での取り組ませ方を紹介します。
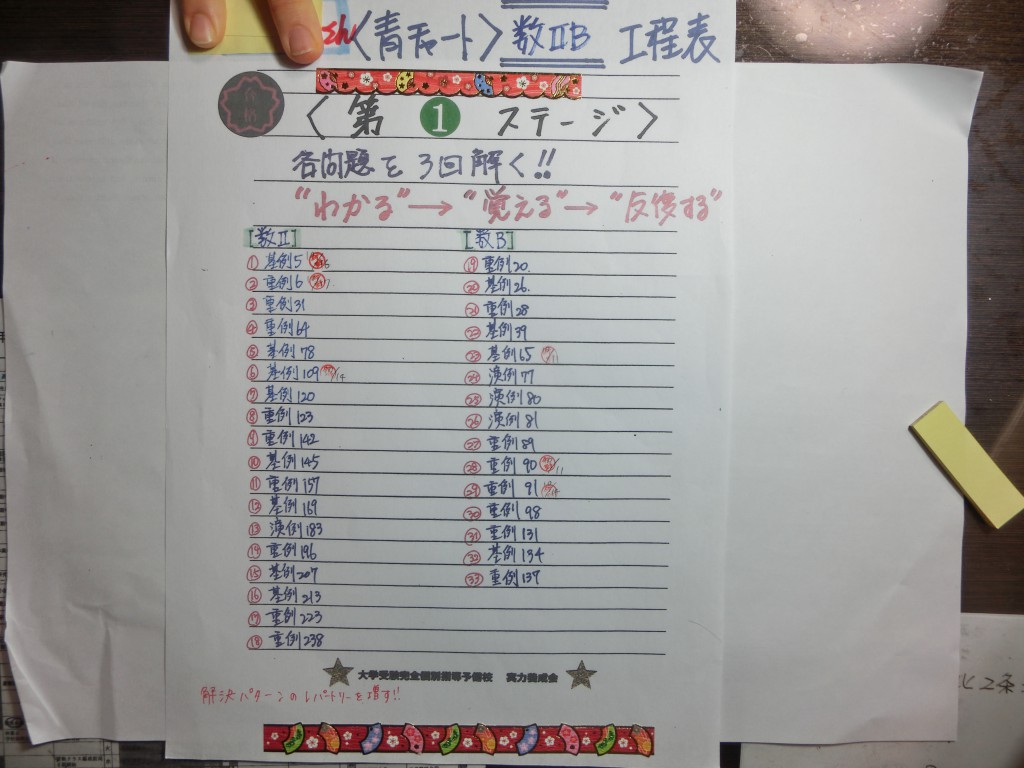
★通称“青チャート工程表”です。
生徒一人一人の状況、すなわち、克服すべき領域、課題点などなどを照らし合わせ、完全
マスターすべき問題を私が厳選し、それを一覧表にまとめ、毎日一題、専用ノートに解かせます。解いた日にちを工程表に書きこみます。
指導日に、毎回チェックし及びフォローのための解説をいれていきます・・これがしっかりとした演習です。
★生徒は、”青チャート工程表”にのっとって、A4の専用ノートにこのように演習していきます。
★生徒がしっかりと取り組めるかどうか?
それは、指示を出す側の、指示の出し方、チェックの仕方次第です。
★この生徒は、高2生です。意識は高いです。このように意識の高い生徒に対してでも、ここまで、こまかく指示をいれるんです!!
★『しっかりとした演習をしましす』 『高みを目指して指導します』 なんて、誰でも口で言うのは簡単です。実力養成会は、口だけじゃありません。
今日も、最後まで、読んでいただき、ありがとうございました。