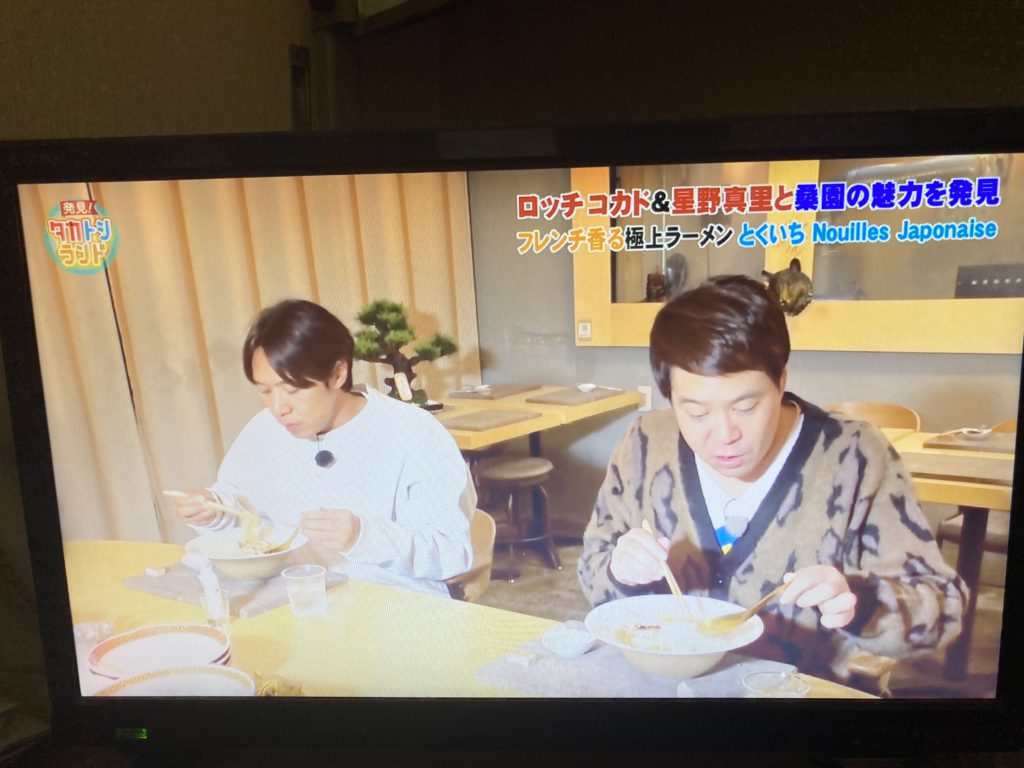
キッカケはこのテレビ番組でした。
桑園の中央卸売市場内にあります。
見ての通りの行列です・・・・・行列のできるお店は、かならずその理由があります。
観光客が多いですが、常連さんと思われる方もいました。
ラーメン屋さん?と思うようなとてもオシャレな店内です。
特製塩らーめん+小ライスです!!
見ての通りの”ビジュアル”です。
昆布とコンソメのだしで作った”泡”・・・・・これで味変を楽しみます!!
まさしく、黄金のスープ!!
函館『あじさい』のスープを気持ち程度濃くした感じです。
かなり上品な味わいです・・・ラーメンというより高級フレンチのスープって感じです。
独特の麺です、全粒粉。
ストレートで割と固めです、スープに見事に合ってます。
鶏のチャーシューです!!
チャーシューの概念が根底から崩されました・・・”うまい”の一言。
いやぁ~・・・・・・感動の味です!!
完成度が極めて高いです!!
有名シェフの作った、完成度が極めて高い、スキのないラーメン!! って感じです。
最後まで、読んでいただき、ありがとうございました。