-
Category / カテゴリー
-
Recent Articles / 最近の記事5件
- 2026/2/4
◆函館五島軒のビーフシチュー - 2026/2/4
◆実力養成会通信 第3139号 ”東京理科大学” の巻 - 2026/2/3
北大院試対策『工学部』対応は可能ですが・・・ - 2026/2/3
実力養成会通信 第3138号 ”昨日の『保護者通信』より” の巻 - 2026/2/2
たかがブログ、されどブログ。
- 2026/2/4
-
Archive / アーカイブ
ニュース・ブログ
大学入試の問題に良くあることです。
見た目は、ベクトルの問題、しかし解いていくにつれ・・・・・・
『これって結局2次関数の最大最小の問題?』
もしくは、見た目は、空間図形・・・・・結局は、2次方程式の解の配置の問題?
これらは、北大2次頻出です。
こういったタイプの典型問題・・・・
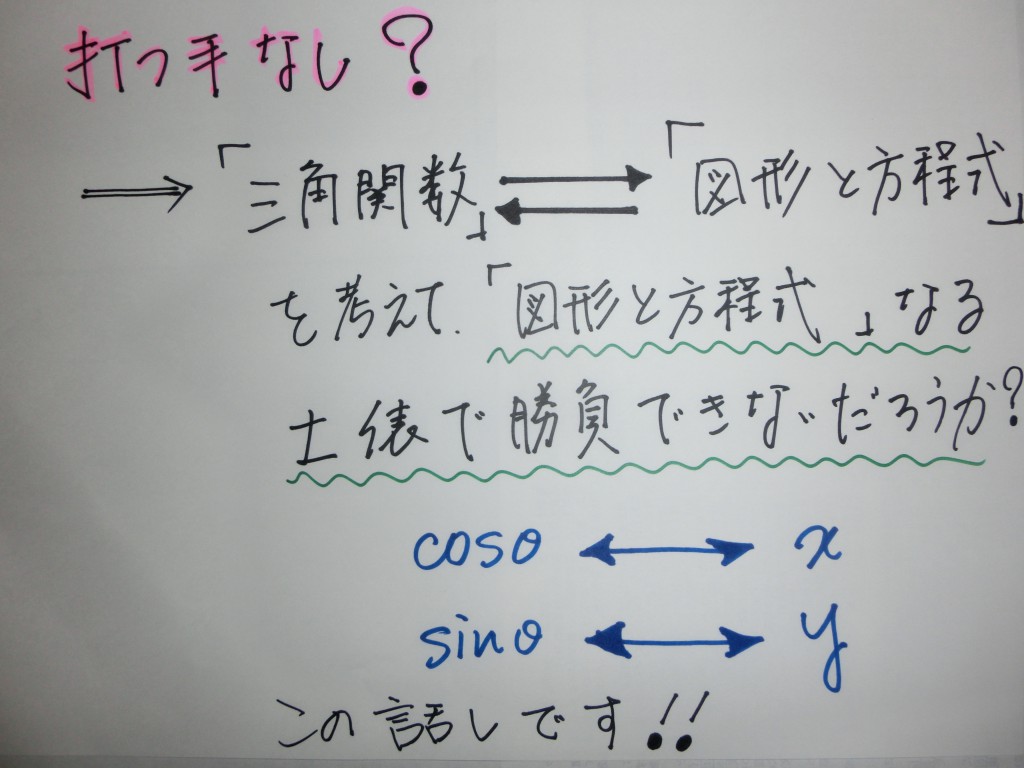
『図形と方程式』 ⇒ 『三角関数』
χ=cosθ、y=sinθ・・・・・とパラメーター表示するタイプです。
『三角関数』の土俵で処理すると、様々な公式(武器)が使え、より有利な状況で処理でき
るわけです。
さて、今回紹介するのが、この逆パターン。
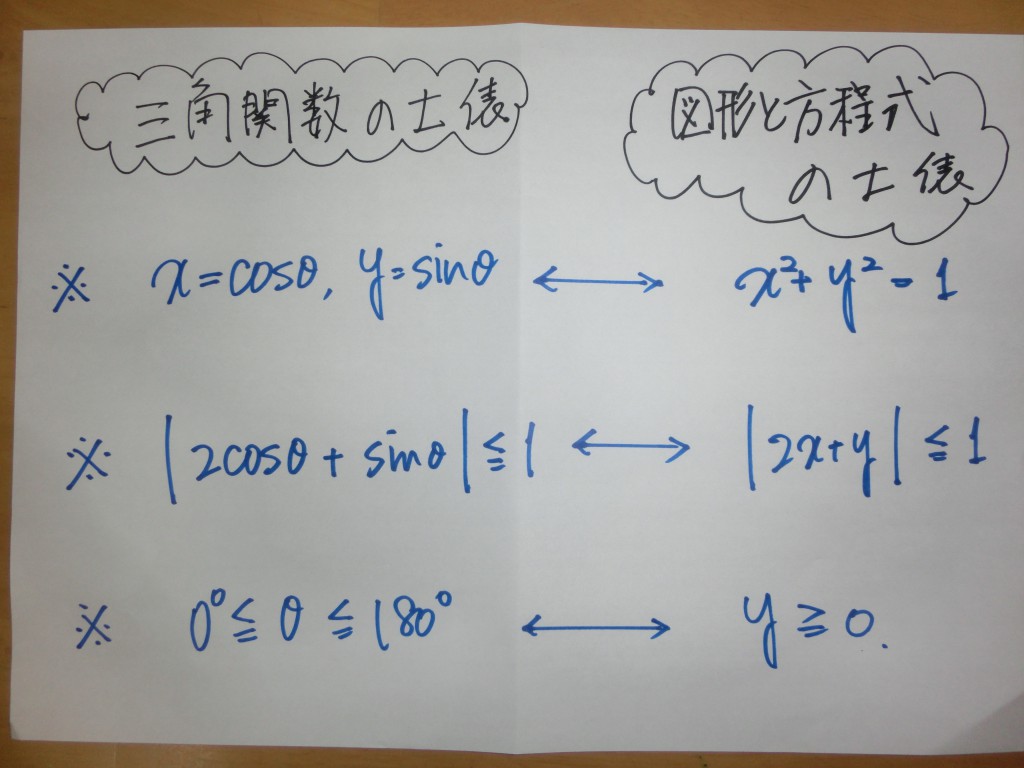
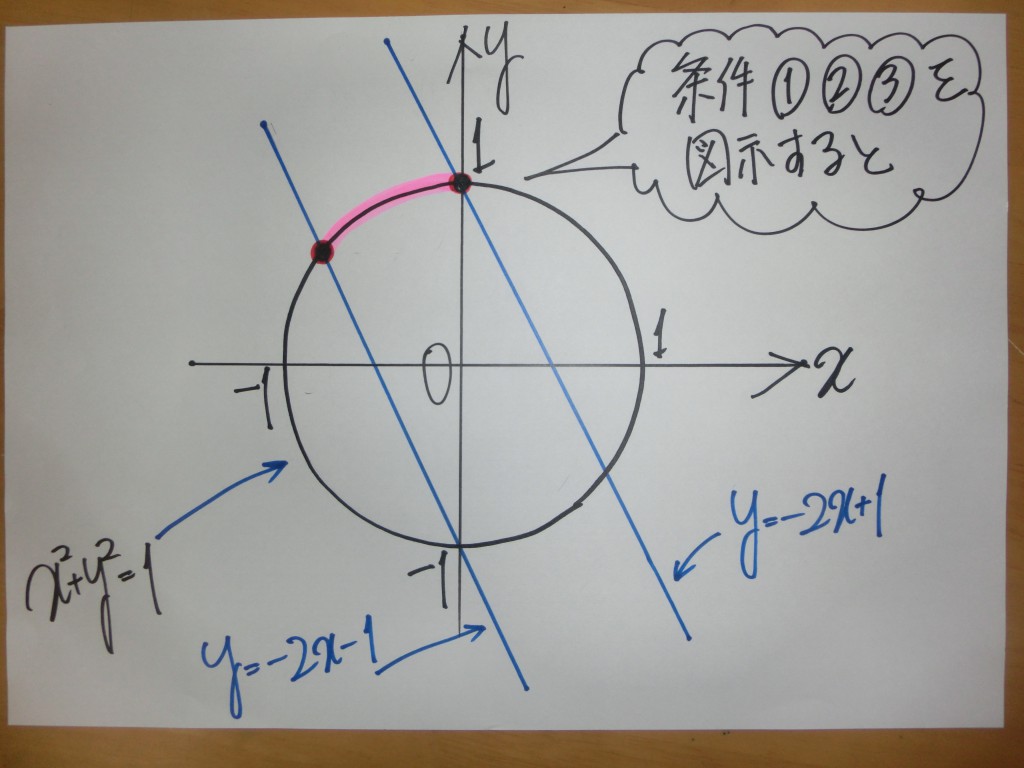
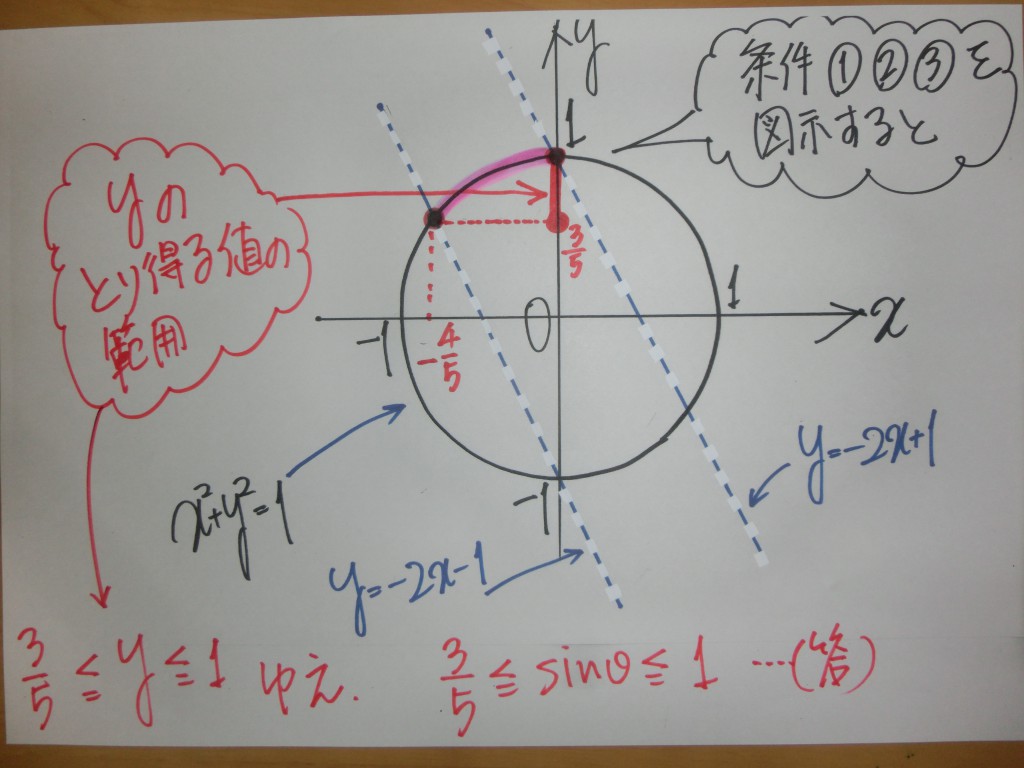
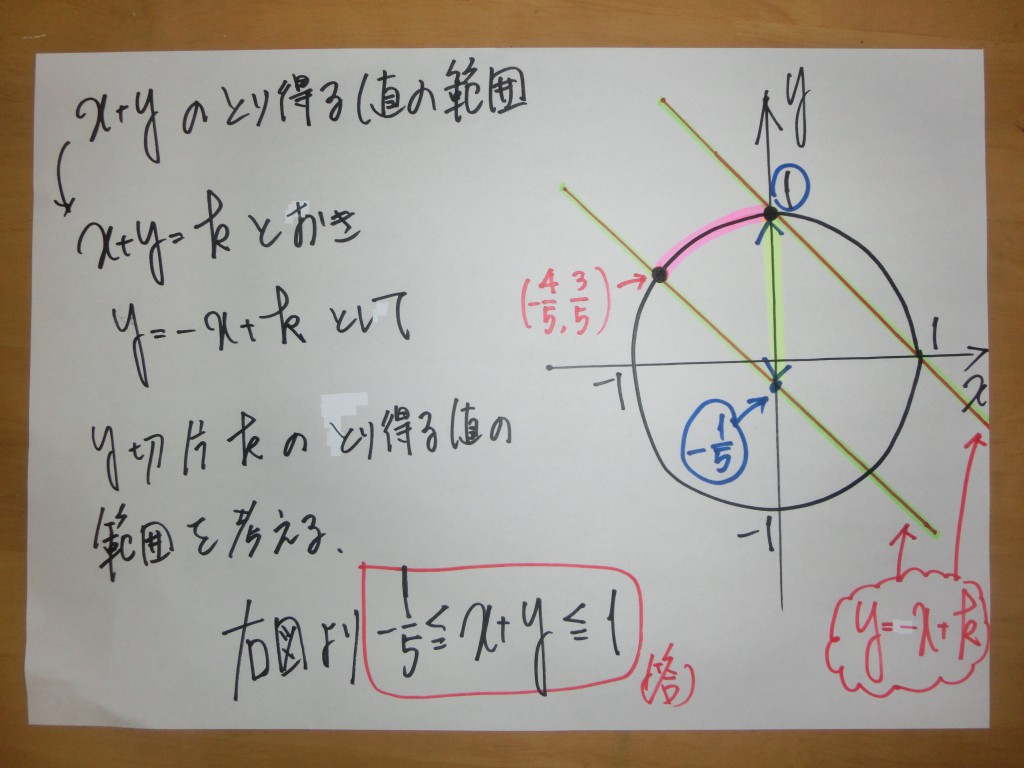
『三角関数』を『図形と方程式』の土俵で処理するというタイプです。
『三角関数』の立場で考えても、ラチが開かない!! ⇒ 『図形の方程式』の分野に問題を書き換えて、処理していきます!!
★さっそく、トライしてみて下さい!!
難易度は、北大文系2次レベルです。
明日のこの通信で、解説を入れます!!
今日も、最後まで、読んでいただき、ありがとうございました。
アルキメデスは、お風呂に入ってる時、湯船にいっぱいになったお湯があふれ出ると同時
に自分の体が軽くなったのを感じて『浮力の原理』を発見したと言いわれてます。
ニュートンは、庭に生えてるリンゴの木から実が落ちるのを見て『万有引力の法則』を
発見しました。
これらは、あまりにも有名なエピソードで『偶然の産物』と紹介されてます。
しかし、決して『偶然の産物』ではありません。
アルキメデスにしてもニュートンにしても、常日頃から『体積とは何か?』
『物理現象の基本原理とは何か?』ということを休まず考え続けていたからこそ発見でき
たのです。
これは、ビジネスの世界でも十分言えることです。
高校生、受験生においても、同様です・・・・・
“お風呂のお湯” ”リンゴの木”のようにヒントは意外なところから出てきます。
解決すべき問題を「いったん忘れて」しまったら、せっかくのヒントもヒントとして気
付くことはできません・・・・
休まず、常日頃から、考え続ける・・・・・
今日も、最後まで、読んでいただき、ありがとうございました。
★実力養成会の奥の教室のバルコニーから発見!!
懐かしくなって写真撮らせてもらいました!! 勝手にごめんなさい。
★実は、私、学生時代、ビルの窓拭き清掃のバイトもしてました・・・・
高層ビルではなく、3階・4解のビルです。私の場合は、『ゴンドラ』に乗ってでした。
風が吹けば、かなり揺れるんです・・・・・
★それでも当時(今から35年位前)、日給で8500円もらってたのを記憶してます・・・・
『ゴンドラ』は、2人で乗って、私は、もっぱら、窓を拭く人の助手って感じでした。
窓拭き清掃の方・・・・頑張って下さい!!
窓拭き清掃助手経験者の今野でした・・・・・
今日も、最後まで、読んでいただき、ありがとうございました。
高体連を間近に控えてます。
部活組の生徒は、疲労もかなり蓄積してます・・・・・
そういった中、先日、高2のS君・・・・・・
20:00~指導でした。1930位に、塾到着。
さっそく、前回指導を受けた複素数平面の”回転”の部分を復習してました・・・・・
気付けば、ノートを広げたまま、ぐっすり寝入ってました・・・・・
私の判断でそのまま指導せず帰しました・・・・・・
相当疲れてるようでした。
疲れて、ヘロヘロにながらも、塾に来てくれたわけです。
指導せずに帰らすというのも・・・・と思いましたが、ここで90分指導するより、早く
家に帰らせて、寝させた方が、本人にとってベターと判断しました。
仮に、90分指導したとしても疲れでボーっとして、おそらく、頭の中には、入っていき
ません。
そこで・・・・・
『高体連、終わって、振替にしよう!!』
『今日は、早く帰って、ゆっくり休め!!』って言って帰しました。
この生徒は、疲れて、気力体力ボロボロになりながらも、塾に来てくれました・・・
そこは、最大限、敬意を表したうえで、帰しました・・・・・・
『気持ち』は、あるんだけど、体がついていかないってヤツです。
今日も、最後まで、読んでいただき、ありがとうございました。