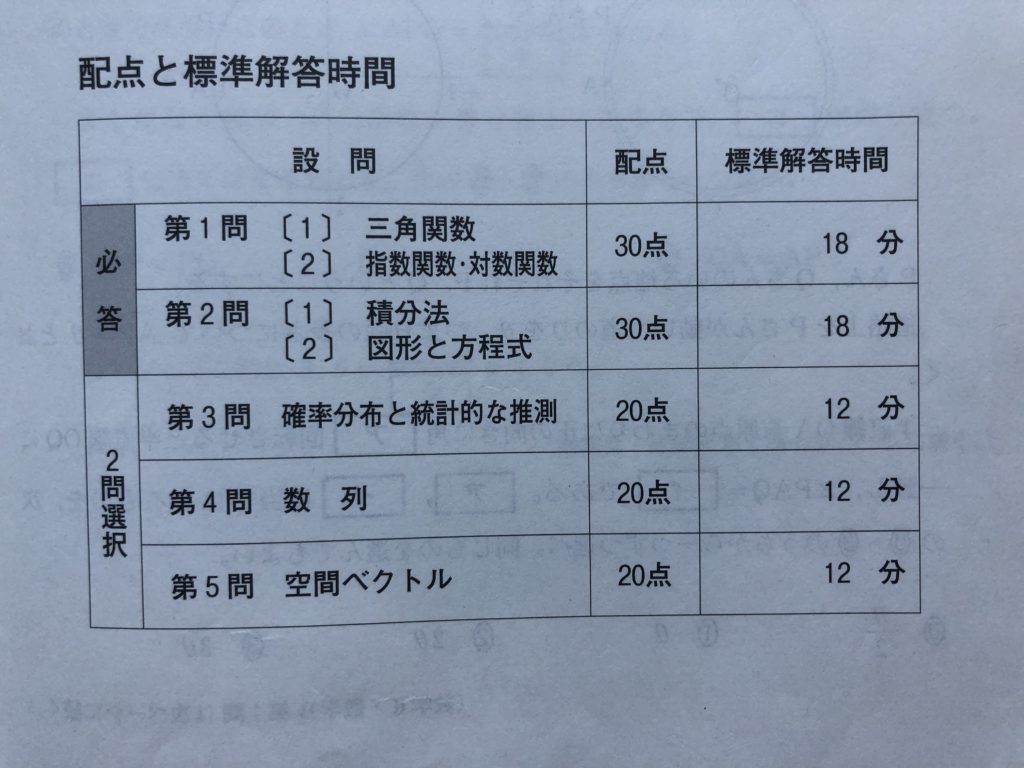
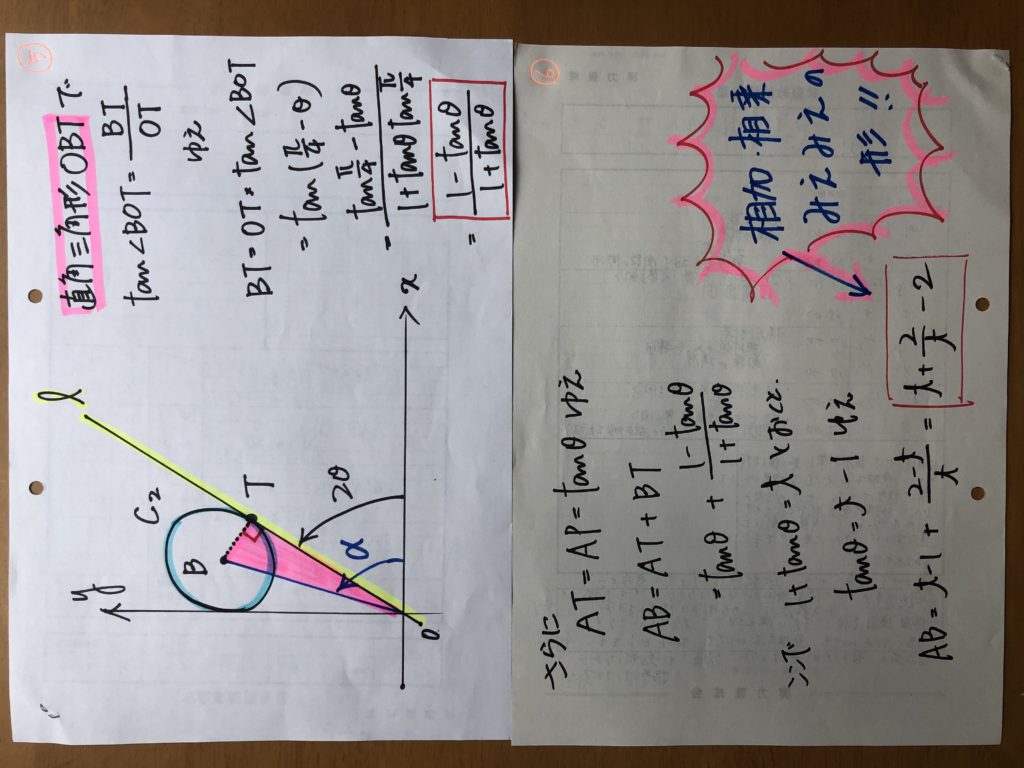
ミニ焚火台・・・・
ソロキャンプの時は、コンパクトな焚火台としてなくてはならないアイテムだ。
たかだか、小さな6枚の側板を組み立てて作る、この”超ミニ焚火台”
しかし、”ヤツ”は、決してあなどれない!!
ということで・・・・
『超ミニ焚火台』で焼き鳥をやいてみた!!
鉄板を敷いたカセットコンロの上にセッティング。
もちろん換気扇を全開にし、窓も全開にしての話だ。
いやいや・・・・一人焼き鳥であれば、これで十分OK!!
一人BBQも、バッチリOK!!
固形燃料で、一人鍋も!!
今度、固形燃料で、一人鍋だ!!
コンパクトなだけに、後片付けもラク!!
炭の火起こしも、カセットコンロで十分だ!!
この他にも、度々ブログに登場してるコイツ!!
この二つがあれば完璧!!
もしもの災害時。
ライフラインがストップした時も、こいつらがいてくれたら頼りになる!!
冬場であれば、十分な暖もとれる。
炭は、夏に購入した9キロ分、まるまるストックしてる・・・・・
みなさんも、ミニ焚火台どうですか?
本日も、最後まで、読んでいただき、ありがとうございました。