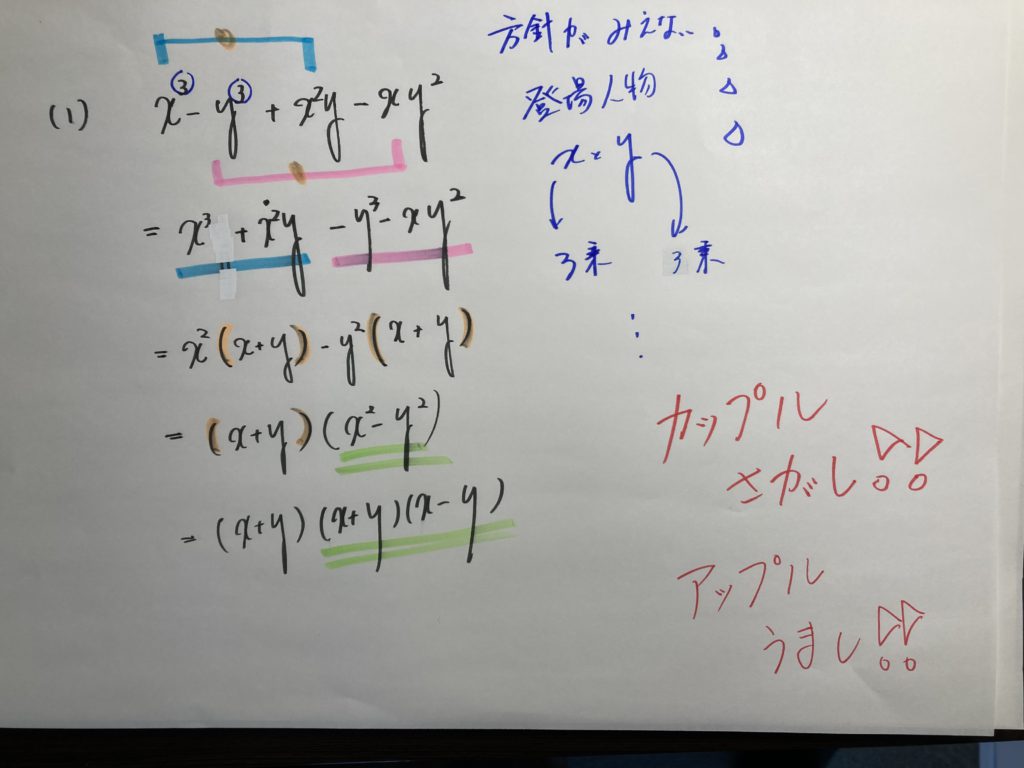-
Category / カテゴリー
-
Recent Articles / 最近の記事5件
- 2026/1/30
2026年、新年度新規受付、定員となりました!! - 2026/1/30
実力養成会通信 第3134号 ”札幌南高で数学学年1位達成!!” の巻 - 2026/1/29
『極王餃子の王将ラーメン』 - 2026/1/29
実力養成会通信 第3133号 ”昨日の保護者通信” の巻 - 2026/1/28
『やりたいことを探しに行く!!』でいいのです。
- 2026/1/30
-
Archive / アーカイブ
ニュース・ブログ
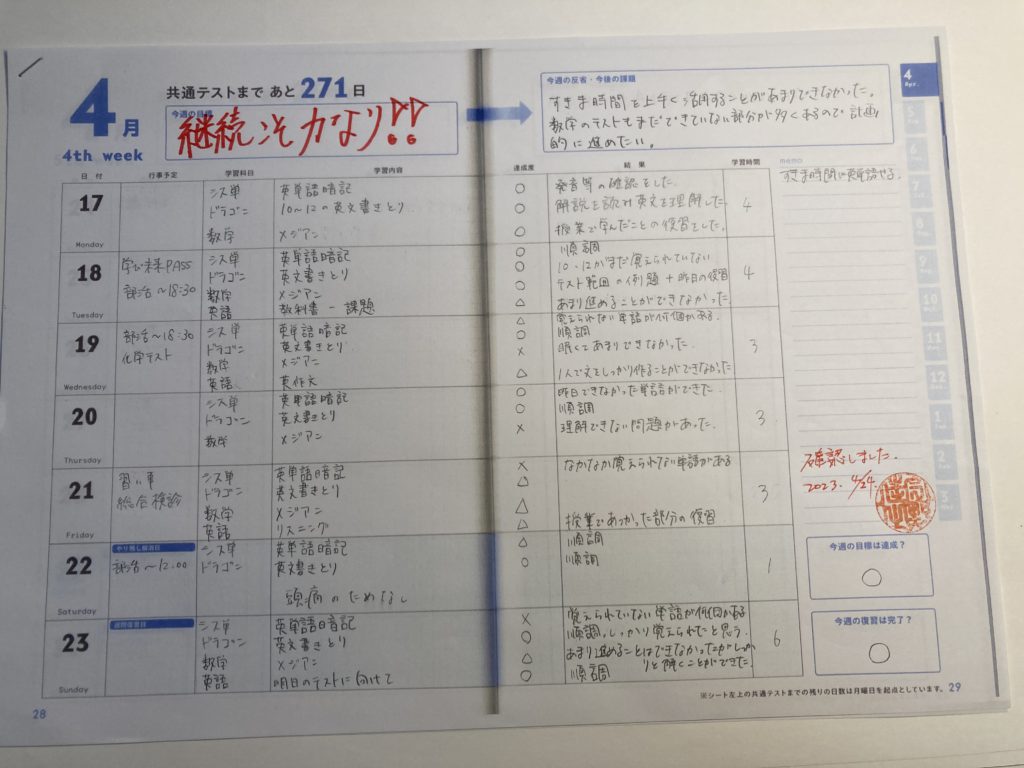
4STEP は、それなりに解ける!!
分からなかったとしても、詳しい解説書を見れば、それなりに分かるでしょう。
とは言え、あくまでも『それなり』
定期考査で言えば、平均点あたりをさまようレベルです。
しかし・・・・そもそも、なぜ、こういう式変形をするのか?
そもそも、その式がどのような意味を持ってるのか?
この辺を突っ込まれると・・・・タジタジ・・・・いゃ、何も返せない・・・・
こういうことってありますね?
具体的に言いましょう!! 例えば、高2生であれば・・
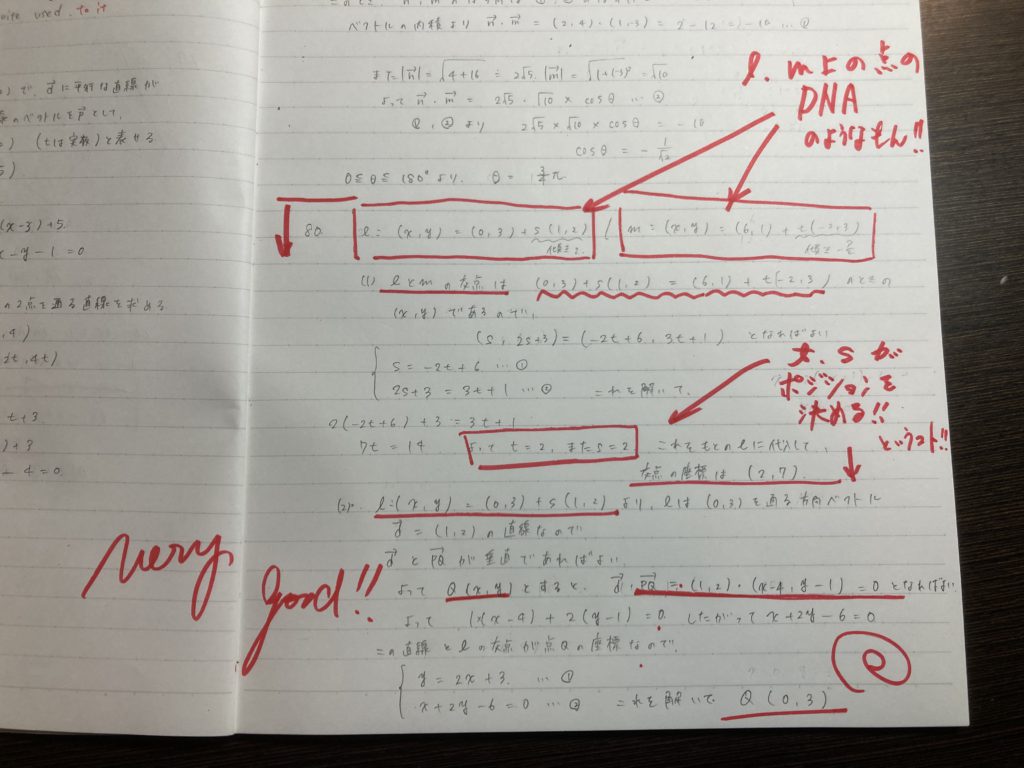
ベクトル方程式 !!
南高生は、優秀です。
公式通りに作業していけば・・・正解になるでしょう。
まぁ、問題の流れ・・を読めば・・”着地点”は、南高校生なら予想はつくでしょう。
がっ、しかぁ~しっ!!
キミたちは、本当に納得して解いてますか?
ただ、公式に当てはめて、正解になっただけで【理解したつもり】になってますね?
結局・・・・自分を誤魔化してるだけでは?
では、この問題・・・・本当に分かってますか?
例題をそのままマネて、解いてるだけになってませんか?
不等式 2 ≦ k ≦ 3 の図形的意味を説明できますか?
公式に当てはめ、機械的に解いて、正解・・・・
これを”理解した”と自分を誤魔化してはダメ!!
私は、こういった部分は、絶対に見逃しません!!
本日も最後まで、読んでいただき、ありがとうございました。