私は、普段から、生徒に対して、
『なぜ、そうなるのか?・・・・ここを強く意識しなさい!!』
『問題と向き合う時、常に”なぜ?” と突っ込みを入れなさい!!』
と言い続けてます!!
昨日の実力養成会通信に続き・・・・
”なぜ” に対する ”明確な説明” ”明確な理由” の一つの例をご紹介させていただ
きます。
ある数Ⅲの教科書です・・・・“当たり前”のこととして書かれてます!!
◆
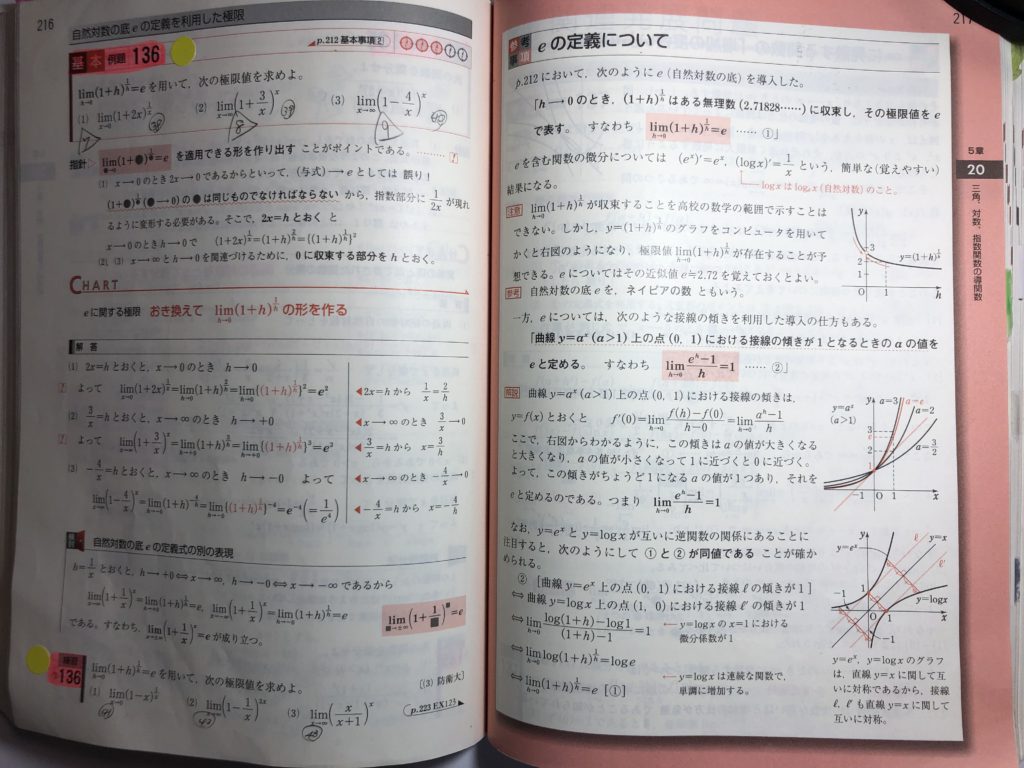
数Ⅲ青チャートに書かれてる『eの定義について』・・
ちなみに”参考事項”という紹介のされ方です!!
これを読んで、果たして、生徒は、”腹にストンって” 落とし込みはできないでしょう。
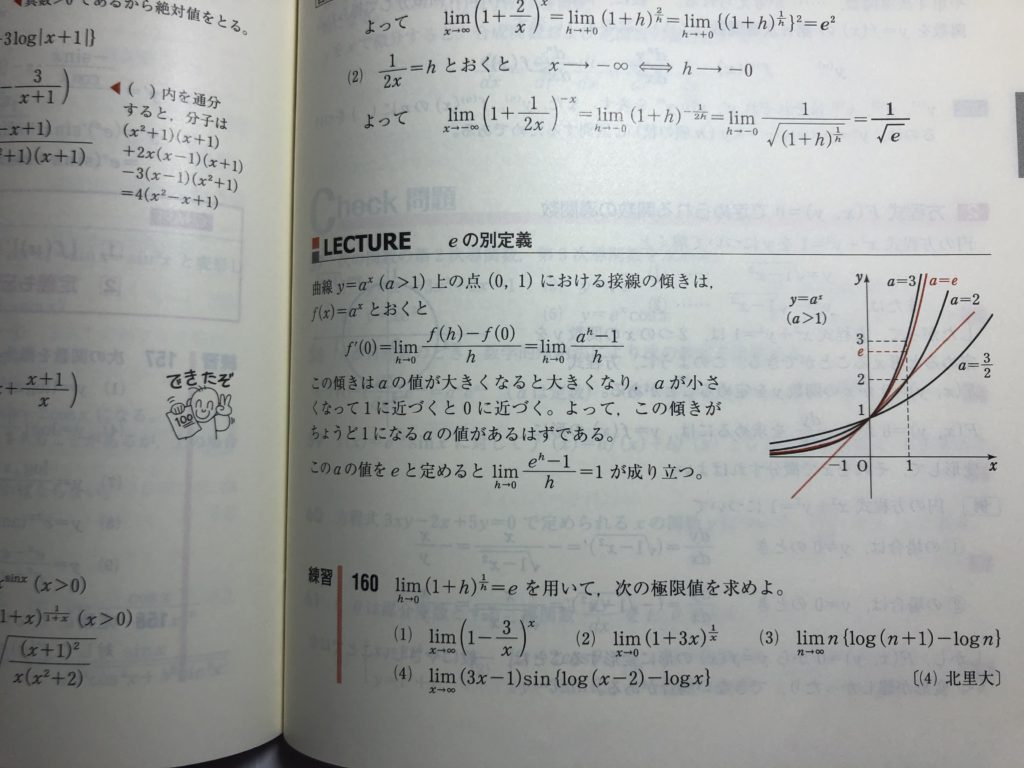
数Ⅲ赤チャートにも書かれてますが・・『レクチャー、eの別定義』という扱いです!!
フォーカスゴールドに書かれてある『eについて』
『コラム』という形で紹介されてます!!
このフォーカスゴールドの説明であれば、
優秀な生徒であれば、”腑に落ちる” と思います。
教科書では、結果だけ切り取った形で当たり前のように書かれてます!!
青チャート、赤チャートでは、”発展事項” 的な感じで、申し訳程度の記載。
フォーカスゴールドでも、”コラム” という扱い・・・・・・・・・・・・
私は、この『e』に関しては、かなり踏み込んで、指導しています。
大学数学の領域まで踏み込みます。
なぜならば、
『eを深く理解することは、微積を深く理解すること』という指導理念があるから、
さらに言えば、
『本質の根底理解こそ、数学上達の一番の近道』と確信してるからです!!
明日の通信で、核心部分をご紹介させていただきます。
今日も、最後まで、読んでいただき、ありがとうございました。